TidyQuant - Analise financeira no R
Pacotes
Para realizar as análises de performance das ações negociadas na B3 vamos utilizar o pacote tidyquant.
Dados
Os dados abaixo possuem uma série de informações sobre as empresas negociadas no B3, com atributos de valor de abertura, fechamento, fechamento ajustado e volume negociado para cada dia do período entre Janeiro de 2019 e Março de 2021. Temos ainda informações sobre o setor e subsetor da economia que a empresa atua.
Para nossa análise, vamos trabalhar apenas com o valor de fechamento ajustado das ações.
O pacote TidyQuant fornece uma função bastante conveniente para baixar dados de ações com apenas o nome do ticker. A função é a tq_get e poderiamos baixar as ações da Vale, Itaú e Petrobras com o seguinte código:
tickers <- c("ITSA3.SA", "PETR3.SA", "VALE3.SA")
tickers %>%
tq_get(get = "stock.prices",
from = "2021-01-02",
to = "2021-3-01") %>%
head(10) %>%
knitr::kable()## Registered S3 method overwritten by 'tune':
## method from
## required_pkgs.model_spec parsnip| symbol | date | open | high | low | close | volume | adjusted |
|---|---|---|---|---|---|---|---|
| ITSA3.SA | 2021-01-04 | 12.35 | 12.43 | 12.08 | 12.24 | 131500 | 11.99251 |
| ITSA3.SA | 2021-01-05 | 12.24 | 12.24 | 11.60 | 12.14 | 522600 | 11.89453 |
| ITSA3.SA | 2021-01-06 | 12.13 | 12.43 | 12.00 | 12.23 | 400500 | 11.98271 |
| ITSA3.SA | 2021-01-07 | 12.31 | 12.73 | 12.24 | 12.61 | 278500 | 12.35503 |
| ITSA3.SA | 2021-01-08 | 12.60 | 12.77 | 12.24 | 12.50 | 233900 | 12.24725 |
| ITSA3.SA | 2021-01-11 | 12.50 | 12.50 | 12.02 | 12.09 | 247600 | 11.84554 |
| ITSA3.SA | 2021-01-12 | 12.09 | 12.54 | 11.85 | 12.22 | 302200 | 11.97292 |
| ITSA3.SA | 2021-01-13 | 12.22 | 12.38 | 12.06 | 12.17 | 117400 | 11.92393 |
| ITSA3.SA | 2021-01-14 | 12.25 | 12.55 | 12.17 | 12.55 | 223500 | 12.29625 |
| ITSA3.SA | 2021-01-15 | 12.43 | 12.44 | 12.07 | 12.07 | 127700 | 11.82595 |
Contudo, como o objetivo é analisar todas as ações que fazem parte da B3 durante o período entre 2019 e março de 2021 (o que é um procedimento bastante lento), vou importar manualmente estes dados, que foram previamente baixados utilizando a própria função tq_get, e tratados a fim de informar o setor e subsetor de atuação da empresa.
df <- read_csv("empresas_b3_2019_2021.zip") %>%
mutate(Data = as.Date(Data)) %>%
filter(Atributo == "Adj Close") %>%
filter(!is.na(Valor)) %>%
select(-Incluir)##
## -- Column specification --------------------------------------------------------
## cols(
## Data = col_date(format = ""),
## Atributo = col_character(),
## Empresa = col_character(),
## Valor = col_double(),
## Setor = col_character(),
## Subsetor = col_character(),
## Segmento = col_character(),
## Nome = col_character(),
## Ticker = col_character(),
## Incluir = col_double()
## )df %>%
head() %>%
knitr::kable()| Data | Atributo | Empresa | Valor | Setor | Subsetor | Segmento | Nome | Ticker |
|---|---|---|---|---|---|---|---|---|
| 2019-01-02 | Adj Close | CSAN3.SA | 34.20791 | Petróleo, Gás e Biocombustíveis | Petróleo, Gás e Biocombustíveis | Exploração, Refino e Distribuição | COSAN | CSAN3.SA |
| 2019-01-03 | Adj Close | CSAN3.SA | 34.72534 | Petróleo, Gás e Biocombustíveis | Petróleo, Gás e Biocombustíveis | Exploração, Refino e Distribuição | COSAN | CSAN3.SA |
| 2019-01-04 | Adj Close | CSAN3.SA | 34.52411 | Petróleo, Gás e Biocombustíveis | Petróleo, Gás e Biocombustíveis | Exploração, Refino e Distribuição | COSAN | CSAN3.SA |
| 2019-01-07 | Adj Close | CSAN3.SA | 34.01627 | Petróleo, Gás e Biocombustíveis | Petróleo, Gás e Biocombustíveis | Exploração, Refino e Distribuição | COSAN | CSAN3.SA |
| 2019-01-08 | Adj Close | CSAN3.SA | 34.38997 | Petróleo, Gás e Biocombustíveis | Petróleo, Gás e Biocombustíveis | Exploração, Refino e Distribuição | COSAN | CSAN3.SA |
| 2019-01-09 | Adj Close | CSAN3.SA | 37.19751 | Petróleo, Gás e Biocombustíveis | Petróleo, Gás e Biocombustíveis | Exploração, Refino e Distribuição | COSAN | CSAN3.SA |
A base de dados possui informações para 286 empresas, divididas em 11 setores e 42 subsetores. Temos informações de janeiro de 2019 a março de 2021.
df %>% summarise(`Total de Empresas` = n_distinct(Nome),
`Total de Setores` = n_distinct(Setor),
`Total de Subsetores` = n_distinct(Subsetor),
`Data de Início` = min(Data),
`Data Final` = max(Data)) %>%
mutate(across(everything(), as.character)) %>%
pivot_longer(everything()) %>%
rename("Atributo" = 1, "Valor" = 2) %>%
knitr::kable()| Atributo | Valor |
|---|---|
| Total de Empresas | 286 |
| Total de Setores | 11 |
| Total de Subsetores | 42 |
| Data de Início | 2019-01-02 |
| Data Final | 2021-03-01 |
Retorno Mensal
Para realizar as comparações propostas, precisamos transformar os preços de fechamento em retornos.
A função tq_transmute permite calcular o retorno mensal para o valor de fechamento ajustado da ação. Para isto, precisamos indicar qual a variável que sofrerá a transformação (Valor), qual a transformação utilizada (mutate_fun = periodReturn) e qual a periodicidade do cálculo (period = "monthly").
Vamos guardar as informações de retorno das ações no objeto Ra.
Ra <- df %>%
select(Data, Empresa, Valor) %>%
group_by(Empresa) %>%
tq_transmute(select = Valor,
mutate_fun = periodReturn,
period = "monthly",
col_rename = "Ra")
Ra %>%
head() %>%
knitr::kable()| Empresa | Data | Ra |
|---|---|---|
| CSAN3.SA | 2019-01-31 | 0.2434172 |
| CSAN3.SA | 2019-02-28 | -0.0155440 |
| CSAN3.SA | 2019-03-29 | -0.0240274 |
| CSAN3.SA | 2019-04-30 | 0.0989447 |
| CSAN3.SA | 2019-05-31 | 0.0277442 |
| CSAN3.SA | 2019-06-28 | -0.0210013 |
Essa base de dados possui três colunas: Data, que representa o último dia do mês, a coluna Ra, que exibe o retorno mensal e Empresa, o ticker de cada empresa.
Como os retornos normalizam os valores, podemos realizar comparações entre diferentes setores, apenas para entender como as empresas foram afetadas pela Covid-19:
Ra %>%
left_join(df %>% select(Empresa, Setor), by = "Empresa") %>%
group_by(Setor, Data) %>%
summarise(Ra = mean(Ra)) %>%
ggplot(aes(x = Data, y = Ra, color = Setor)) +
geom_line() +
geom_vline(xintercept = as.Date("2020-03-01"), linetype = 2,
color = "grey20") +
labs(y = "Retorno Mensal Médio", y = "data",
title = "Retorno Mensal Médio por Setor da B3, 2019 - 2021") +
facet_wrap(~Setor, nrow = 3) +
theme_minimal() +
theme(legend.position = "none",
axis.text.x = element_text(angle = 45))## `summarise()` has grouped output by 'Setor'. You can override using the `.groups` argument.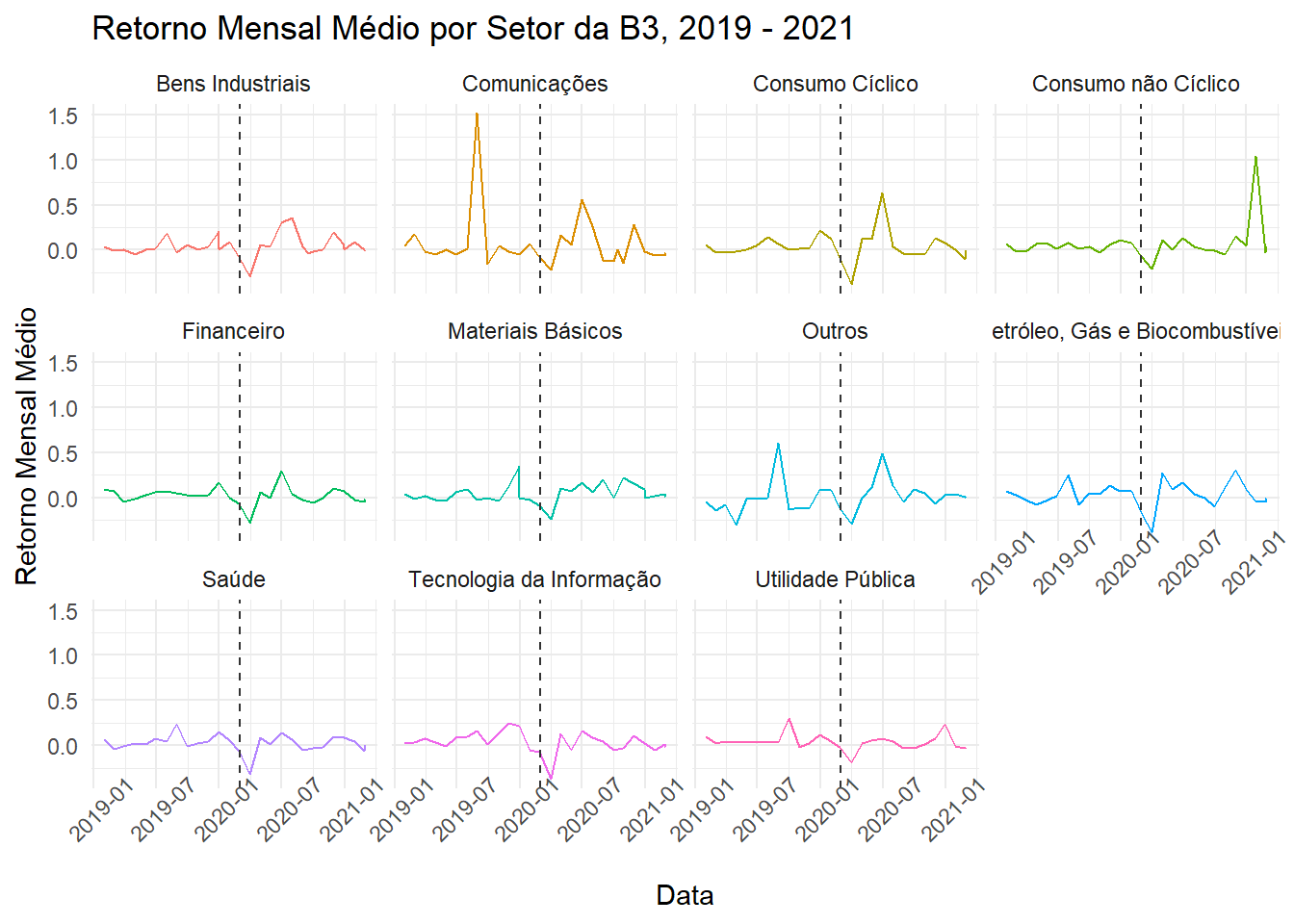
Retorno Livre de Risco
A fim de comparar o comportamento dos retornos de cada ação, precisamos de um grupo de comparação, também chamado de baseline. Como grupo de comparação, vamos utilizar o valor negociado do Índice Bovespa (BVSP).
Podemos utilizar a função tq_get para obter os dados do ticker ^BVSP para o mesmo período de análise e transformar as informações de fechamento em retorno mensal, e unir com as informações de Ra:
Rb <- "^BVSP" %>%
tq_get(get = "stock.prices",
from = "2019-01-02",
to = "2021-03-01") %>%
tq_transmute(select = adjusted,
mutate_fun = periodReturn,
period = "monthly",
col_rename = "Rb")
RaRb <-
left_join(Ra,
Rb,
by = c("Data" = "date"))
RaRb %>%
head() %>%
knitr::kable()| Empresa | Data | Ra | Rb |
|---|---|---|---|
| CSAN3.SA | 2019-01-31 | 0.2434172 | 0.0701226 |
| CSAN3.SA | 2019-02-28 | -0.0155440 | -0.0185843 |
| CSAN3.SA | 2019-03-29 | -0.0240274 | -0.0017681 |
| CSAN3.SA | 2019-04-30 | 0.0989447 | 0.0098307 |
| CSAN3.SA | 2019-05-31 | 0.0277442 | 0.0070262 |
| CSAN3.SA | 2019-06-28 | -0.0210013 | 0.0405751 |
Razões de Risco
Aqui vamos apresentar cinco razões de risco bastante populares: Alpha, Beta, o Desvio-padrão, R-squared e a Razão de Sharpe.
Razão de Sharpe
A Razão de Sharpe é comumente utilizada como uma medida de retorno por unidade de risco, e tem a seguinte fórmula
onde
Quando maior a razão Sharpe, melhor é a combinação de risco e retorno.
Abaixo, um exemplo de como funciona a Razão de Sharp:
| Portfólio A | Portfólio B | |
|---|---|---|
| Retorno | 7,9% | 6,9% |
| Risco | 5,5% | 3,2% |
| Taxa livre de risco | 2,0% | 2,0% |
| Razão de Sharpe |
Portanto, o portifólio B possui uma melhor performance ajustada ao risco do que o portfólio A.
Agora podemos calcular para nosso banco de dados. Vamos utilizar a função tq_performance, que toma os seguintes argumentos: o conjunto de retornos Ra; Rf, que é a taxa livre de risco, p, que é o intervalo de confiança (de 95% no nosso caso) e FUN, que é o valor do denominador (onde utilizaremos o desvio-padrão). Por simplificação vamos usar uma taxa livre de risco de zero.
Ra_Sharpe <- RaRb %>%
filter(!Empresa %in% c('JSLG3.SA', "TIMS3.SA","MGEL3.SA")) %>%
tq_performance(Ra = Ra,
Rb = NULL,
performance_fun = SharpeRatio,
Rf = 0,
p = 0.95,
FUN = "StdDev")
Ra_Sharpe %>%
head() %>%
knitr::kable()| Empresa | StdDevSharpe(Rf=0%,p=95%) |
|---|---|
| CSAN3.SA | 0.3373760 |
| DMMO3.SA | -0.0493056 |
| ENAT3.SA | 0.2675225 |
| RPMG3.SA | 0.1077110 |
| PETR3.SA | 0.0503555 |
| BRDT3.SA | 0.0333009 |
Podemos filtrar para os 10 ativos com maior valor da razão de Sharpe.
Ra_Sharpe %>%
rename(Razao_Sharpe = 2) %>%
arrange(desc(Razao_Sharpe)) %>%
head(10) %>%
knitr::kable()| Empresa | Razao_Sharpe |
|---|---|
| REDE3.SA | 0.9270783 |
| ENEV3.SA | 0.7157285 |
| BAUH4.SA | 0.6367148 |
| WEGE3.SA | 0.5623846 |
| MGLU3.SA | 0.5230350 |
| GPCP3.SA | 0.5103846 |
| BMEB3.SA | 0.4654880 |
| PRIO3.SA | 0.4576669 |
| KEPL3.SA | 0.4574844 |
| RSUL4.SA | 0.4483069 |
CAPM
O pacote TidyQuant também permite estimar o modelo CAPM para as ações. No modelo CAPM podemos fatorar a taxa livre de risco e calcular a seguinte equação:
Para estimar o modelo CAPM, vamos utilizar a função tq_performance novamente, mas agora passando o argumento performance_fun = table.CAPM. Como visto na equação acima, ela apresenta uma série de novos parâmetros: como beta e alpha.
Mas primeiro, vamos gerar as informações da tabela CAPM:
RaRb_capm <- RaRb %>%
# essas empresas possuem informações faltantes e serão excluídas
filter(!Empresa %in% c('JSLG3.SA', "TIMS3.SA","MGEL3.SA")) %>%
tq_performance(Ra = Ra,
Rb = Rb,
performance_fun = table.CAPM)
RaRb_capm %>%
head(10) %>%
knitr::kable()| Empresa | ActivePremium | Alpha | AnnualizedAlpha | Beta | Beta- | Beta+ | Correlation | Correlationp-value | InformationRatio | R-squared | TrackingError | TreynorRatio |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CSAN3.SA | 0.4004 | 0.0291 | 0.4112 | 1.0559 | 0.9035 | 0.7168 | 0.7470 | 0.0000 | 1.4645 | 0.5580 | 0.2734 | 0.4527 |
| DMMO3.SA | -0.7680 | -0.0386 | -0.3761 | 1.7924 | 1.7276 | 1.8920 | 0.3784 | 0.0567 | -0.5953 | 0.1432 | 1.2901 | -0.3737 |
| ENAT3.SA | 0.2178 | 0.0191 | 0.2556 | 1.0081 | 1.1774 | 0.4574 | 0.7035 | 0.0001 | 0.7179 | 0.4949 | 0.3034 | 0.3362 |
| RPMG3.SA | -0.1134 | 0.0455 | 0.7049 | 0.9500 | 1.0682 | -3.3047 | 0.1583 | 0.4400 | -0.0661 | 0.0251 | 1.7155 | -0.0222 |
| PETR3.SA | -0.1499 | -0.0106 | -0.1196 | 1.6813 | 1.6147 | 2.3237 | 0.9135 | 0.0000 | -0.5085 | 0.8344 | 0.2948 | -0.0350 |
| BRDT3.SA | -0.1319 | -0.0085 | -0.0970 | 1.1569 | 1.3428 | 0.4957 | 0.8242 | 0.0000 | -0.5573 | 0.6792 | 0.2366 | -0.0379 |
| PRIO3.SA | 1.5305 | 0.0917 | 1.8663 | 2.1954 | 2.5173 | 3.4174 | 0.7369 | 0.0000 | 2.2576 | 0.5430 | 0.6780 | 0.7249 |
| UGPA3.SA | -0.2222 | -0.0169 | -0.1851 | 1.3715 | 0.9149 | 1.5346 | 0.8320 | 0.0000 | -0.7752 | 0.6922 | 0.2867 | -0.1004 |
| LUPA3.SA | -0.0058 | 0.0071 | 0.0881 | 1.4102 | 1.6683 | 1.4490 | 0.6870 | 0.0001 | -0.0129 | 0.4720 | 0.4488 | 0.0601 |
| OSXB3.SA | 0.9830 | 0.1097 | 2.4882 | 1.3732 | 1.6842 | 4.5573 | 0.2529 | 0.2125 | 0.6445 | 0.0640 | 1.5253 | 0.7275 |
Agora vamos entender cada um dos parâmetros do modelo CAPM, a começar pelo Beta.
Beta (
Ele representa o risco sistêmico ou a volatilidade de uma ação específica comparada com o risco sistêmico do mercado como um todo. De maneira geral, um Beta igual a 1 representa uma atividade bastante correlacionada com o mercado. Adicionar uma ação com beta igual a 1 a um portfólio não adiciona nenhum risco a ele. Um beta menor que a unidade significa que a ação é menos volátil que a média do mercado, de modo que sua inclusão reduz o risco médio do porfólio. Por exemplo, ações de empresas de utilidades públicas tendem a ter um beta baixo.
Já empresas com beta maior que a unidade indicam que o preço da ação é teoricamente mais volátil que o mercado. Se uma ação possui beta igual a 1,2 podemos assumir que ele é 20% mais volátil que o mecado. Ações de tecnologia tendem a ter maiores betas que o benchmark de mercado. Isto indica que sua adição ao portfólio aumenta o risco (mas também pode aumentar o retorno esperado).
Vamos observar os maiores valores de Beta:
RaRb_capm %>%
select(Empresa, Beta) %>%
arrange(desc(Beta)) %>%
head(10) %>%
left_join(df %>% select(Empresa, Setor), by = "Empresa") %>%
distinct()## # A tibble: 10 x 3
## # Groups: Empresa [10]
## Empresa Beta Setor
## <chr> <dbl> <chr>
## 1 TXRX3.SA 6.06 Consumo Cíclico
## 2 TCSA3.SA 5.16 Consumo Cíclico
## 3 MWET3.SA 3.43 Bens Industriais
## 4 CEPE3.SA 2.86 Utilidade Pública
## 5 TEKA3.SA 2.78 Consumo Cíclico
## 6 RCSL3.SA 2.51 Bens Industriais
## 7 EUCA3.SA 2.49 Materiais Básicos
## 8 PRIO3.SA 2.20 Petróleo, Gás e Biocombustíveis
## 9 CVCB3.SA 2.13 Consumo Cíclico
## 10 VVAR3.SA 2.11 Consumo CíclicoPodemos ver que entre as empresas com maior volatilidade, temos empresas de Petróleo, Consumo Cíclico e até mesmo uma de Utilidade Pública.
Algumas ações possuem beta negativo, isso reflete o fato de que estas empresas são espelhos do mercado. Quando o mercado está em alta, ela está em baixa, e vice-versa. Alguns exemplos:
RaRb_capm %>%
select(Empresa, Beta) %>%
arrange(Beta) %>%
head(10) %>%
left_join(df %>% select(Empresa, Setor), by = "Empresa") %>%
distinct()## # A tibble: 10 x 3
## # Groups: Empresa [10]
## Empresa Beta Setor
## <chr> <dbl> <chr>
## 1 ODER4.SA -3.09 Consumo não Cíclico
## 2 NORD3.SA -0.989 Bens Industriais
## 3 CEGR3.SA -0.386 Utilidade Pública
## 4 CEED3.SA -0.313 Utilidade Pública
## 5 JOPA3.SA -0.301 Consumo não Cíclico
## 6 LUXM3.SA -0.265 Bens Industriais
## 7 BMIN3.SA -0.230 Financeiro
## 8 AHEB3.SA -0.196 Consumo Cíclico
## 9 SLCE3.SA -0.0809 Consumo não Cíclico
## 10 REDE3.SA -0.0638 Utilidade PúblicaContudo, um valor pequeno de beta apenas informa que a volatilidade do preço é baixa. Mas uma empresa pode ter pequenas variações de preço e estar em uma tendência de longo prazo de baixa. Assim, adicionar uma ação com tendência de baixa com um beta pequeno diminui o risco do portfólio apenas se o investidor define risco estritamente em termos de volatilidade, em vez de potencial para perdas. Da mesma foram, uma ação com beta elevado mas que está em um tendência de alta vai aumentar o risco do portfólio, mas também irá adicionar valor.
Portanto é preciso utilizar o beta com cuidado, sempre em conjunto com outras medidas. Assim, o beta pode ser util para avaliar o risco de curto prazo de uma ação, não sendo muito útil quando se deseja fazer investimentos de longo prazo, uma vez que a volatilidade da ação pode mudar bastante no longo prazo.
Temos ainda:
O Beta Bull ou
O Beta Bear ou
Alpha ou Alpha de Jenson
Alpha representa o intercepto da equação de regressão no CAPM, e reflete o grau com que o retorno de uma ação está em linha (ou excede) o retorno gerado pelo mercado. Assim, o alpha representa os retornos sobre o investimento que não são o resultado de um movimento geral de mercado. O alpha de Jensen especificamente, inclui um componente de risco ajustado nas suas contas.
Uma ação com alpha igual a zero possui retornos em linha com o presente no mercado. Por outro lado, um alpha negativo indica que a ação não gera retornos na mesma taxa que o setor como um todo.
RaRb_capm %>%
select(Empresa, Alpha) %>%
arrange(desc(Alpha)) %>%
head(10) %>%
left_join(df %>% select(Empresa, Setor), by = "Empresa") %>%
distinct() %>%
knitr::kable()| Empresa | Alpha | Setor |
|---|---|---|
| ODER4.SA | 0.5959 | Consumo não Cíclico |
| TXRX3.SA | 0.5785 | Consumo Cíclico |
| GPAR3.SA | 0.4351 | Utilidade Pública |
| MWET3.SA | 0.2814 | Bens Industriais |
| NORD3.SA | 0.2795 | Bens Industriais |
| TCSA3.SA | 0.2692 | Consumo Cíclico |
| MMXM3.SA | 0.2243 | Materiais Básicos |
| CEPE3.SA | 0.1966 | Utilidade Pública |
| TEKA3.SA | 0.1922 | Consumo Cíclico |
| TELB3.SA | 0.1709 | Comunicações |
Tracking Error
Medidas de risco absoluto como analisadadas anteriormente calculam o risco do portfólio e do benchmarking calculados separadamente, para posterior comparação. O tracking error é um exemplo de uma medida de risco relativa, cujo foco é no retorno em excesso do portfólio contra o benchmarking. A variabilidade de retorno em excesso é calculada usando o desvio-padrão, e é chamada de tracking error.
Sua fórmula é dada por
Ele representa a diferença entre a performance observada entre uma posição (ação ou porfólio) e do seu benchmarking. Assim, mede a consistência de um porfólio contra um benchmarking ao longo de um dado período. Mesmo portfólios que são perfeitamente indexados contra um benchmarking se comportam diferentemente de um benchmarking. Assim, o tracking error é utilizado para quantificar essas diferenças.
Se o retorno do investimento for baixo mas possui um valor alto de tracking error, este é um sinal de que uma mudança de portfólio é necessária.
Se o tracking error for elevado significa que o retorno do portfólio é mais volátil ao longo do tempo e não tão consiste em bater o benchmarking.
RaRb_capm %>%
select(Empresa, TrackingError) %>%
arrange(desc(TrackingError)) %>%
head(10) %>%
left_join(df %>% select(Empresa, Setor), by = "Empresa") %>%
distinct() %>%
knitr::kable()| Empresa | TrackingError | Setor |
|---|---|---|
| TXRX3.SA | 10.0619 | Consumo Cíclico |
| ODER4.SA | 9.5899 | Consumo não Cíclico |
| GPAR3.SA | 7.4202 | Utilidade Pública |
| TCSA3.SA | 5.7209 | Consumo Cíclico |
| MWET3.SA | 5.5682 | Bens Industriais |
| CEPE3.SA | 3.9775 | Utilidade Pública |
| MMXM3.SA | 3.6660 | Materiais Básicos |
| TELB3.SA | 3.3057 | Comunicações |
| TEKA3.SA | 3.2550 | Consumo Cíclico |
| NORD3.SA | 3.1530 | Bens Industriais |
Razão de Informação
A razão de informação é similar a Razão de Sharpe, só que ao invés de comparar retornos absolutos, temos retornos em excesso, e em vez de risco absoluto, temos risco relativo (tracking error). Geralmente são calculados utilizados retornos anuais. Assim, a Razão de Informação mostra o quanto um portfólio excedeu um benchmarking.
Abaixo, um exemplo hipotético em que o índice tenha retorno anualizado de -1,5%:
| Portfólio | Retorno anualizado | Tracking Error | Razão de Informação |
|---|---|---|---|
| A | 13% | 8% | |
| B | 8% | 4,5% |
Assim, apesar do portfólio B tem retornos menores que A, ele tem melhor RI, em parte, porque ele tem menor desvio padrão ou tracking error, que significa menos risco e mais consistência do portfólio relativo ao benchmarking.
RaRb_capm %>%
select(Empresa, InformationRatio) %>%
arrange(desc(InformationRatio)) %>%
head(10) %>%
left_join(df %>% select(Empresa, Setor), by = "Empresa") %>%
distinct() %>%
knitr::kable()| Empresa | InformationRatio | Setor |
|---|---|---|
| ENEV3.SA | 4.2181 | Utilidade Pública |
| BAUH4.SA | 2.7556 | Consumo não Cíclico |
| GPCP3.SA | 2.7504 | Materiais Básicos |
| WEGE3.SA | 2.7054 | Bens Industriais |
| MGLU3.SA | 2.4541 | Consumo Cíclico |
| PRIO3.SA | 2.2576 | Petróleo, Gás e Biocombustíveis |
| CSNA3.SA | 1.7580 | Materiais Básicos |
| HAPV3.SA | 1.7489 | Saúde |
| IGBR3.SA | 1.7337 | Financeiro |
| KEPL3.SA | 1.6978 | Bens Industriais |
R Quadrado
O R quadrado informa o quão correlacionado um ativo ou portfólio está com o benchmarking. R-squared mede o grau com que a performance de um portfólio pode ser atribuida a performance de um índice de benchmarking.
RaRb_capm %>%
select(Empresa, `R-squared`) %>%
arrange(desc(`R-squared`)) %>%
head(10) %>%
left_join(df %>% select(Empresa, Setor), by = "Empresa") %>%
distinct() %>%
knitr::kable()| Empresa | R-squared | Setor |
|---|---|---|
| PETR3.SA | 0.8344 | Petróleo, Gás e Biocombustíveis |
| BBAS3.SA | 0.8130 | Financeiro |
| SMLS3.SA | 0.8095 | Consumo Cíclico |
| CVCB3.SA | 0.8068 | Consumo Cíclico |
| VIVA3.SA | 0.7947 | Consumo Cíclico |
| IGTA3.SA | 0.7832 | Financeiro |
| JPSA3.SA | 0.7800 | Financeiro |
| MULT3.SA | 0.7759 | Financeiro |
| BBDC3.SA | 0.7630 | Financeiro |
| CYRE3.SA | 0.7475 | Consumo Cíclico |