Previsão de Séries Semanais com Pacote Modeltime
Introdução
Duas das técnicas de série temporais mais comumente utilizadas para realizar previsões são os modelos (S)ARIMA e o Exponential Smoothing (ETS). Modelos ARIMA tendem a produzir resultados interessantes com séries mensais, trimestrais e anuais. O modelo ETS atribui pesos exponencialmente decrescentes aos valores defasados da série para estimar seus valores atuais, e funcionam bem com dados diários, mensais e anuais.
Para séries diárias, se o período de análise compreende mais de um ano, é possível que além da sazonalidade semanal usual destes dados (frequência de 7), em que existe uma relação entre os dias da semana, seja preciso permitir a presença de sazonalidade anual. Nesta situação o modelo ETS produzirá resultados inconsistentes.
O problema é ainda maior para dados semanais. Segundo Hyndman, criador do pacote forecast, modelos ARIMA e ETS tem dificuldades em produzir boas previsões para séries semanais devido a sua sazonalidade peculiar, dado que o período de sazonalidade é de em média
Seja com dados diários muito longos ou para dados semanais, uma alternativa é o uso do modelo TBATS. Este modelo é uma extensão do ETS que adiciona uma série de transformações Box-Cox, séries Fourier com coeficientes variantes no tempo além de correção de erro ARMA. Ele é especialmente útil para produzir previsão de séries temporais com múltiplos períodos de sazonalidade, sazonalidade de altíssima-frequência, sazonalidade não-inteira (como a frequência de 52,18 discutida acima) e múltiplos efeito calendários.
Outra solução é utilizar termos de Fourier, que são úteis em lidar com sazonalidade. Uma forma de utilizar estes termos é estimando modelos que aceitam covariadas externas como parte da especificação. É o caso dos modelos (S)ARIMAX e do modelo de Regressão com Erros ARIMA (RegARIMA). De modo geral, ambos possuem capacidade preditiva semelhante, mas o RegARIMA tem a vantagem adicional de que os coeficientes das covariadas tem a interpretação usual dos modelos de regressão. Se interpretabilidade for algo importante, a escolha parece natural. Abaixo a notação usual do RegARIMA:
onde
Na seção seguinte vamos apresentar uma base de dados semanal, e estimar o conjunto de modelos discutido acima com uso do pacote Modeltime. Este pacote é construído acima do tidymodels e possui uma série de funções convenientes para lidar com dados de série temporal.
Banco de Dados
Abaixo temos uma série de oferta semanal de gasolina para os Estados Unidos. Os dados podem ser obtidos no site da EIA.
library(tidyverse)
library(tidymodels)
library(modeltime)
library(timetk)
library(skimr)
library(tidyquant)
df <- read_csv("gasolina.csv") %>%
mutate(date = as.Date(date))
df %>% plot_time_series(date, gasoline)É possível observar que a série é bastante longa, com 745 observações, e tendo inicio em Janeiro de 1991 e em 10 de Abril de 2005.
Criação de Base de Treinamento e Teste
O pacote rsample permite a construção de bases de treinamento e teste. Atribuimos 80% da série original à base de treinamento (596 pontos) e 20% à base de teste (149 observações).
set.seed(123)
tbl_treinamento_teste <- df %>%
initial_time_split(prop = 0.8)
tbl_treinamento_teste %>%
tk_time_series_cv_plan() %>%
plot_time_series_cv_plan(date, gasoline)Pré-Processamento dos Dados
Agora vamos especificar uma receita_simples utilizando o pacote recipes para ser aplicado aos modelos univariados que não aceitam covariadas. Em receita_fourier vamos utilizar a coluna date para construir termos de Fourier. Especificamente vamos criar termos com frequência de
receita_simples <- recipe(gasoline ~ date, training(tbl_treinamento_teste))
receita_fourier <- recipe(gasoline ~ date, training(tbl_treinamento_teste)) %>%
step_fourier(date, period = 365.25/7, K = 2)Abaixo vemos as quatro variáveis criadas. O banco de dados pode ser extraído com uso da função prep e juice, para preparar a receita na base de treinamento e extrair o data.frame.
receita_fourier %>%
prep() %>%
juice() %>%
head()## # A tibble: 6 x 6
## date gasoline date_sin52.18_K1 date_cos52.18_K1 date_sin52.18_K2
## <date> <dbl> <dbl> <dbl> <dbl>
## 1 1991-01-06 6621 0.0816 0.997 0.163
## 2 1991-01-13 6433 0.201 0.980 0.393
## 3 1991-01-20 6582 0.317 0.948 0.601
## 4 1991-01-27 7224 0.429 0.903 0.775
## 5 1991-02-03 6875 0.534 0.845 0.903
## 6 1991-02-10 6947 0.632 0.775 0.979
## # ... with 1 more variable: date_cos52.18_K2 <dbl>Talvez um gráfico das variáveis ilustre melhor o que elas pretendem captar. Estas variáveis serão incluídas no modelo RegARIMA como variáveis exógenas.
receita_fourier %>% prep() %>% juice() %>%
pivot_longer(cols = "gasoline":"date_cos52.18_K2") %>%
ggplot(aes(x = date, y = value)) +
geom_line() +
facet_wrap(~name, scales = "free_y") +
theme_bw()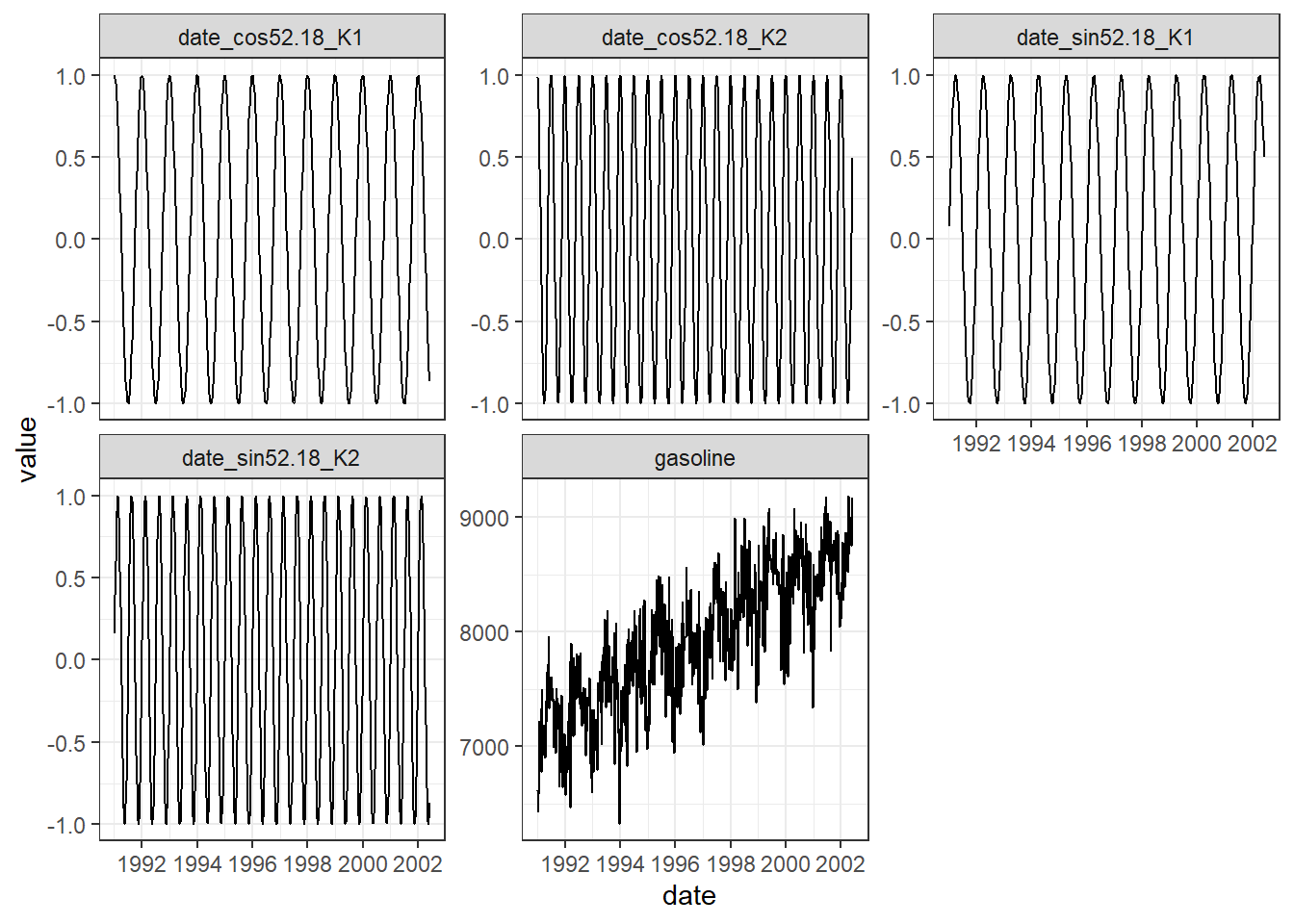
Estimação dos Modelos
Podemos definir os quatro modelos discutidos utilizando o pacote Modeltime. De modo semelhante ao pacote tidymodels, precisamos declarar o modelo em dois passos:
Primeiro chamamos uma função específica, como
arima_reg()para modelos arima. Nela especificamos os parâmetros e hiperparâmetros do modelo.Depois especificamos a implementação do algorítimo que iremos utilizar. Para estimar um Arima podemos utilizar o pacote
arimacomset_engine("arima")ou utilizar a implementação do pacoteauto.arima, usando a funçãoset_engine("auto_arima").
# modelo arima e regressao com erros arima
modelo_arima <- arima_reg() %>%
set_engine("auto_arima")
# modelo ets
modelo_ets <- seasonal_reg() %>%
set_engine("stlm_ets")
# modelo tbats
modelo_tbats <- seasonal_reg() %>%
set_engine("tbats")Abaixo criamos um workflow com o pacote workflow, que especifica três objetos: (1) os dados a serem utilizados, (2) o pré-processamento a ser conduzido e (3) o a especificação do modelo a ser estimado.
# modelo arima
workflow_arima <- workflow() %>%
add_recipe(receita_simples) %>%
add_model(modelo_arima) %>%
fit(training(tbl_treinamento_teste))
# modelo regressao com erros arimas
workflow_regarima <- workflow() %>%
add_recipe(receita_fourier) %>%
add_model(modelo_arima) %>%
fit(training(tbl_treinamento_teste))
# modelo ets
workflow_ets <- workflow() %>%
add_recipe(receita_simples) %>%
add_model(modelo_ets) %>%
fit(training(tbl_treinamento_teste))
# modelo tbats
workflow_tbats <- workflow() %>%
add_recipe(receita_simples) %>%
add_model(modelo_tbats) %>%
fit(training(tbl_treinamento_teste))Uma das funções mais úteis do pacote Modeltime é o modeltime_table, que permite construir listas de modelos que podem ser facilmente interagidas. É possível calibrar as estimativas na base de teste, criar medidas de performance, além de produzir previsões para um grande número de modelos de uma única vez.
tbl_modelos <- modeltime_table(
workflow_arima,
workflow_regarima,
workflow_ets,
workflow_tbats
)Agora podemos calibrar o modelo informando a base de teste e os dados observados. É importante destacar que a operação abaixo aplica as transformações passadas por recipe para a base de teste da mesma forma que o workflow() aplicou transformações à base de treinamento.
A tabela de calibração mostra os 4 modelos estimados: um ARIMA(0,1,2), um modelo de Regressão com Erros ARIMA(0,1,2), um modelo de ETS(A,A,N) (um modelo simples com erros aditivos) e um modelo TBATS. Perceba que o pacote TBATS tenta automaticamente encontrar a frequência da série, a definindo como 13,6, o que equivale a uma sazonalidade trimestral. Talvez isso comprometa os resultados do TBATS, assumindo que 52,18 seja o valor mais adequado. Seria possível ainda fixar o valor da frequência utilizando a opção seasonal_reg(seasonal_period_1 = 52.18).
tbl_calibracao <- tbl_modelos %>%
modeltime_calibrate(new_data = testing(tbl_treinamento_teste))
tbl_calibracao ## # Modeltime Table
## # A tibble: 4 x 5
## .model_id .model .model_desc .type .calibration_data
## <int> <list> <chr> <chr> <list>
## 1 1 <workflow> ARIMA(0,1,2) Test <tibble [149 x 4~
## 2 2 <workflow> REGRESSION WITH ARIMA(0,1,2) ERR~ Test <tibble [149 x 4~
## 3 3 <workflow> SEASONAL DECOMP: ETS(A,N,N) Test <tibble [149 x 4~
## 4 4 <workflow> TBATS(1, {2,2}, -, {<13,6>}) Test <tibble [149 x 4~Com a tabela de calibração podemos gerar as previsões para o período de teste.
tbl_calibracao %>%
modeltime_forecast(new_data = testing(tbl_treinamento_teste),
actual_data = df) %>%
plot_modeltime_forecast()E agora as medidas de desempenho. O modelo de Regressão com Erros Arima e o Modelo ETS produziram as previsões com o menores valores de MAPE. Porém, os valores previstos pelo modelo ETS são bem estranhos.
tbl_calibracao %>%
modeltime_accuracy(new_data = testing(tbl_treinamento_teste)) %>%
select(.model_desc, mape, rmse) %>%
kableExtra::kable()| .model_desc | mape | rmse |
|---|---|---|
| ARIMA(0,1,2) | 2.789477 | 302.3442 |
| REGRESSION WITH ARIMA(0,1,2) ERRORS | 2.035896 | 230.1507 |
| SEASONAL DECOMP: ETS(A,N,N) | 2.856568 | 310.7472 |
| TBATS(1, {2,2}, -, {<13,6>}) | 3.409583 | 374.5799 |
Assim, Nosso modelo ajustado com RegARIMA possui 2 pares de termos de Fourier e pode ser escrito como
Como foi discutido, é possível melhorar o modelo utilizando mais termos de Fourier. O Professor Hyndman inclui 12 termos na sua análise. É interessante notar que a Regressão com Erros Arima produziu resultados até superiores aqueles obtidos pelo TBATS.
Por curiosidade, o resultado com
receita_fourier_12 <- recipe(gasoline ~ date, training(tbl_treinamento_teste)) %>%
step_fourier(date, period = 365.25/7, K = 12)
fit_12_k <- workflow() %>%
add_recipe(receita_fourier_12) %>%
add_model(modelo_arima) %>%
fit(training(tbl_treinamento_teste)) %>%
modeltime_calibrate(new_data = testing(tbl_treinamento_teste))
fit_12_k %>% modeltime_accuracy(new_data = testing(tbl_treinamento_teste)) %>%
select(.model_desc, mape)## # A tibble: 1 x 2
## .model_desc mape
## <chr> <dbl>
## 1 REGRESSION WITH ARIMA(2,1,1)(1,0,0)[13] ERRORS 1.82E a previsão realizada com
fit_12_k %>%
modeltime_forecast(new_data = testing(tbl_treinamento_teste),
actual_data = df) %>%
plot_modeltime_forecast()