Estimando Demanda e Definindo Preço
Introdução
Vamos supor por simplicidade que o lucro de uma empresa com a vender de um produto é dado por:
\[\pi = (p - c)q - F\]
onde cada produto \(q\) é vendido por um preço \(p\), de modo que cada unidade vendida produz uma receita \(pq\) menos um custo unitário \(cq\), onde \(c\) é o custo marginal de ofertar o produto. Temos ainda um conjunto de custos fixos \(F\) que devem ser pagos pela empresa independentemente de quanto é produzido. Em resumo, se o preço é \(p = \$10\) e o custo marginal é igual a \(c = 4\), cada unidade vendida produz um retorno de \(\$6\). Se a empresa vende 100 unidades e possui um custo fixo de \(F = \$200\), temos um lucro de \(\pi = 6*100 - 200 = \$400\).
Essa equação é uma simplificação e suponhe que o custo marginal não é uma função da quantidade produzida \(q\), como ocorre quando a empresa possui economias de escala. Nessas situações o custo de produção diminui quando a escala de produção se eleva.
Mas, se por um lado o custo não depende da quantidade produzida, por outro, a quantidade produzida pela empresa depende do preço. Assim, o problema da empresa é maximizar lucro na seguinte forma:
\[\max_p \pi = (p-c)q(p) - F\] Das aulas de cálculo sabemos que o ponto máximo de uma função côncava é aquele onde a derivada da função é igual a zero. Logo:
\[\frac{\delta \pi}{\delta p} = 0 \rightarrow q + pq'(p) + cq'(p) = 0\]
Agora organizando a equação para \(p\) ficamos com um preço que maximiza o lucro da empresa. Vamos chama-lo de preço ótimo:
\[p^* = c - \frac{q}{q'(p)}\]
Este preço depende do custo marginal \(c\), mas também depende de um segundo termo que é a razão da quantidade pela derivada da quantidade. O denominador \(\frac{\delta q}{\delta p}\) é termo o mais interessante da expressão, e representa o quanto da quantidade consumida muda em resposta a uma alteração do preço. Este valor é quase sempre negativo, uma vez que aumentos de preços geralmente reduzem a quantidade consumida pelos clientes.
Este termo no denominador também está presente na fórmula da elasticidade-preço da demanda. Um conceito econômico que procura medir a sensibilidade dos clientes a mudanças de preços. Especificamente ele mede o quanto uma mudança percentual nos preços reduz o consumo (percentual) por um produto. Sua fórmula é dada por:
\[\epsilon_p = \frac{\Delta \% Q}{\Delta \% P} = \frac{\delta q}{\delta p} \frac{p}{q}\]
Interpretamos a elasticidade assim: quando o preço sobe 10% e a quantidade consumida cai apenas 2%, dizemos que o produto é pouco sensível a mudanças de preço, ou que ele é inelástico. Mas se o mesmo aumento de preço de 10% reduz a demanda em 12%, dizemos que o aumento de preço provoca uma redução mais que proporcional na quantidade demandada, e que o produto possui uma demanda elástica.
A figura abaixo ilustra a relação entre preço e quantidade por meio de uma curva linear de demanda. Esta curva possui uma inclinação negativa \(\frac{\delta q}{\delta p} < 0\).
library(tidyverse)
# devtools::install_github("andrewheiss/reconPlots")
library(reconPlots)
line1 <- data.frame(y = c(8000, 0), x = c(0, 100))
ggplot(mapping = aes(x = x, y = y)) +
geom_line(data = line1, color = "#FC4E07", size = 1) +
geom_segment(aes(x = -Inf, y = 6400, xend = 20, yend = 6400),
lineend = "round", linejoin = "round", linetype = 2,
size = 0.5) +
geom_segment(aes(x = 20, y = -Inf, xend = 20, yend = 6400),
lineend = "round", linejoin = "round", linetype = 2,
size = 0.5) +
geom_segment(aes(x = -Inf, y = 4800, xend = 40, yend = 4800),
lineend = "round", linejoin = "round", linetype = 2,
size = 0.5) +
geom_segment(aes(x = 40, y = -Inf, xend = 40, yend = 4800),
lineend = "round", linejoin = "round", linetype = 2,
size = 0.5) +
geom_segment(aes(x = -Inf, y = 2400, xend = 70, yend = 2400),
lineend = "round", linejoin = "round", linetype = 2,
size = 0.5) +
geom_segment(aes(x = 70, y = -Inf, xend = 70, yend = 2400),
lineend = "round", linejoin = "round", linetype = 2,
size = 0.5) +
scale_y_continuous(breaks = seq(0,9000,1000)) +
scale_x_continuous(breaks = seq(0,120,10)) +
geom_point(aes(x = 20, y= 6400), size = 2) +
geom_point(aes(x = 40, y= 4800), size = 2) +
annotate("text", x = 20, y = 6800, label = "A") +
annotate("text", x = 30, y = 7000, label = "Elasticidade = 4") +
annotate("text", x = 40, y = 5100, label = "B") +
annotate("text", x = 50, y = 5500, label = "Elasticidade = 1,5") +
annotate("text", x = 70, y = 2700, label = "C") +
annotate("text", x = 80, y = 3000, label = "Elasticidade = 0,43") +
theme_minimal() +
labs(x = "Quantidade", y = "Preço", title = "Curva de Demanda Linear")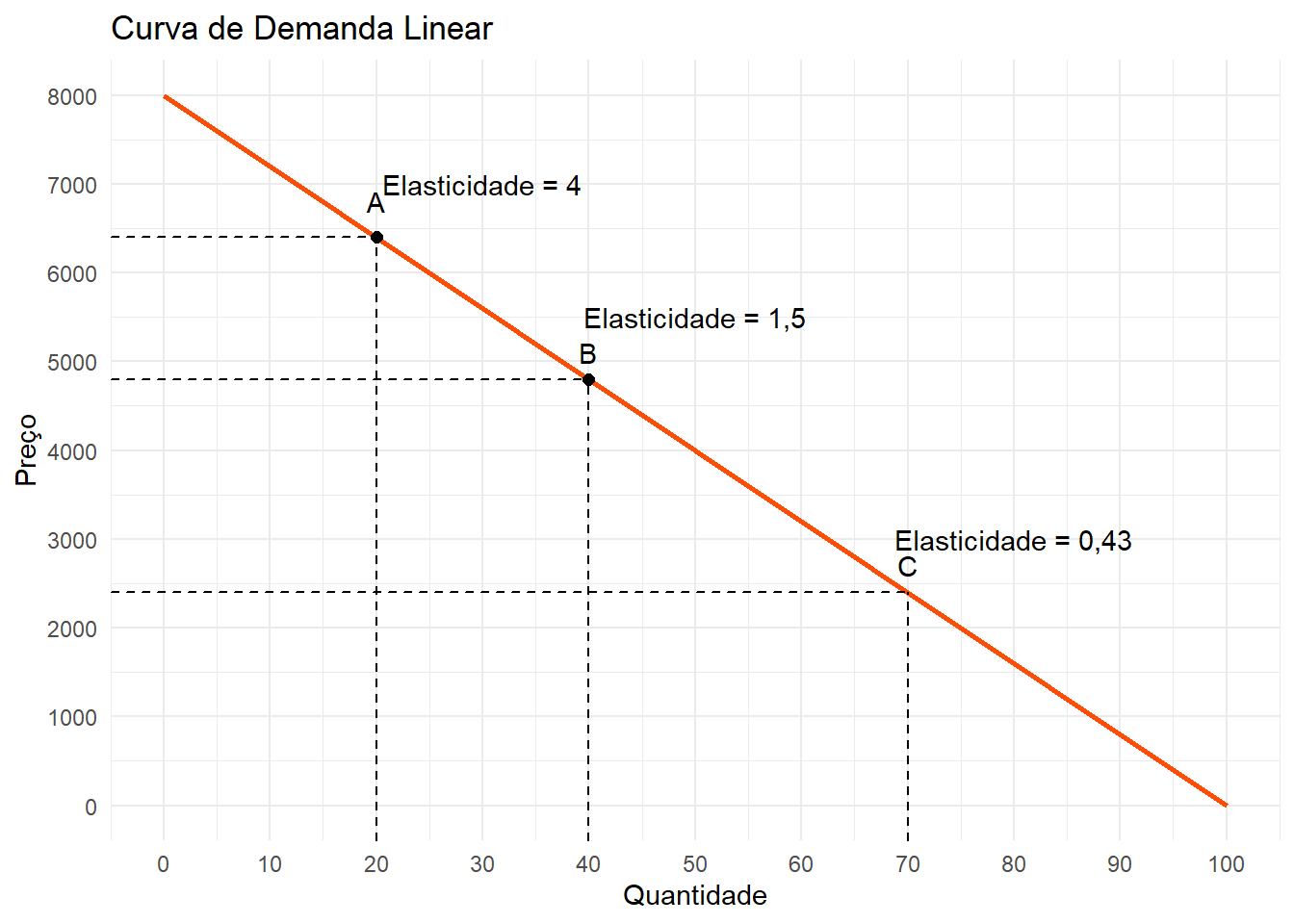
Note que a curva de demanda possui uma inclinação negativa, mas diferentes valores de elasticidade ao longo dela. É intuitivo imaginar que os consumidores são muito mais sensíveis a um aumento de preço de 10% se esse aumento ocorre quando o preço já está muito alto.
Mas também é intuitivo generalizar que se o valor de \(\frac{\delta q}{\delta p}\) é próximo de zero, os consumidores serão em média menos sensíveis a mudanças de preço (demanda inelástica), o que daria uma maior liberdade para a empresa definir um preço \(p*\) mais alto. Do contrário, se o valor de \(\frac{\delta q}{\delta p}\) é um número muito negativo, os consumidores serão sempre muito sensíveis a mudanças nos preços (demanda elástica). Isto porque o segundo termo da equação de \(p^*\) tenderá a zero e o preço ótimo vai se aproximar do custo marginal \(c\) de produzir o bem.
\[p^* = c - \downarrow \frac{q}{q'(p)}\]
Estimando o Preço Ótimo
Mas como estimar o termo \(\frac{\delta q}{\delta p}\) de um produto específico? Com um pouco de cuidado podemos utilizar dados históricos de preço e quantidade para tanto.
Para ilustrar esta possibilidade, vamos produzir um banco de dados sintético (cortesia deste excelente notebook) que representa a decisão de compra de 900 mil usuários durante um periodo de 90 dias. A cada dia 10 mil usuários acessam um site fictício, e metade deles se defrontam com um preço de \(\$ 0.4\); a outra metade é surpreendida com um preço de \(\$ 0.8\).
set.seed(0)
T <- 90 # dias
n_por_dia <- 10000 # usuarios por dia
n <- T * n_por_dia # acessos totais
dia <- sort(rep(seq(1,T), n_por_dia)) # vetor de dias
utilidade_media <- 0.5
coef_preco <- -0.5
preco_maior = 0.8
preco_menor = 0.4A coluna comprou indica se o usuário tomou a decisão de consumir o bem ou não. Esta decisão depende da satisfação que o consumidor espera obter ao comprar o produto (chamado de utilidade na economia), e depende do preço do produto. Assim, divimos a decisão de comprar em três componentes: uma utilidade média comum a todos os usuários, que representa o quão atrativo o bem é para todos os consumidores; uma utilidade específica e aleatória para cada consumidor, que mostra o gosto pessoal de cada indivíduo; e uma sensibilidade ao preço que também é comum a todos (\(-0.5*preco\)). Ao somar estes três componentes, se a utilidade calculada for maior que zero, o usuário decide comprar.
df <- data.frame(dia = dia,
componente_usuario = rnorm(n = n)) %>%
mutate(precos = c(rep(preco_menor, n / 2),
rep(preco_maior, n / 2))) %>%
mutate(utilidade_produto = utilidade_media +
componente_usuario + coef_preco * precos) %>%
mutate(comprou = (utilidade_produto > 0))
df %>% head()## dia componente_usuario precos utilidade_produto comprou
## 1 1 1.2629543 0.4 1.56295428 TRUE
## 2 1 -0.3262334 0.4 -0.02623336 FALSE
## 3 1 1.3297993 0.4 1.62979926 TRUE
## 4 1 1.2724293 0.4 1.57242932 TRUE
## 5 1 0.4146414 0.4 0.71464143 TRUE
## 6 1 -1.5399500 0.4 -1.23995004 FALSEDados na forma de clientes podem ser difíceis de serem obtidos na vida real, apesar de quase sempre permitirem obter resultados mais interessantes. Mas para ilustrar um caso mais geral, podemos trabalhar com dados agregados de compra por dia:
df_diario <- df %>%
# agrupar dados por dia
group_by(dia) %>%
# somar o total de compras e capturar o maior preço do dia
summarise(quantidade = sum(comprou),
precos = max(precos))
df_diario %>%
ggplot(aes(x = dia, quantidade, color = factor(precos))) +
geom_line() +
geom_vline(xintercept = 45, linetype = 'longdash') +
labs(x = "", y = "Quantidade Vendida",
color = "Preço:", title = "Vendas Diárias, 90 dias",
subtitle = "Um Experimento envolvendo o Aumento Drástico do Preço") +
theme_minimal() +
theme(legend.position = 'bottom')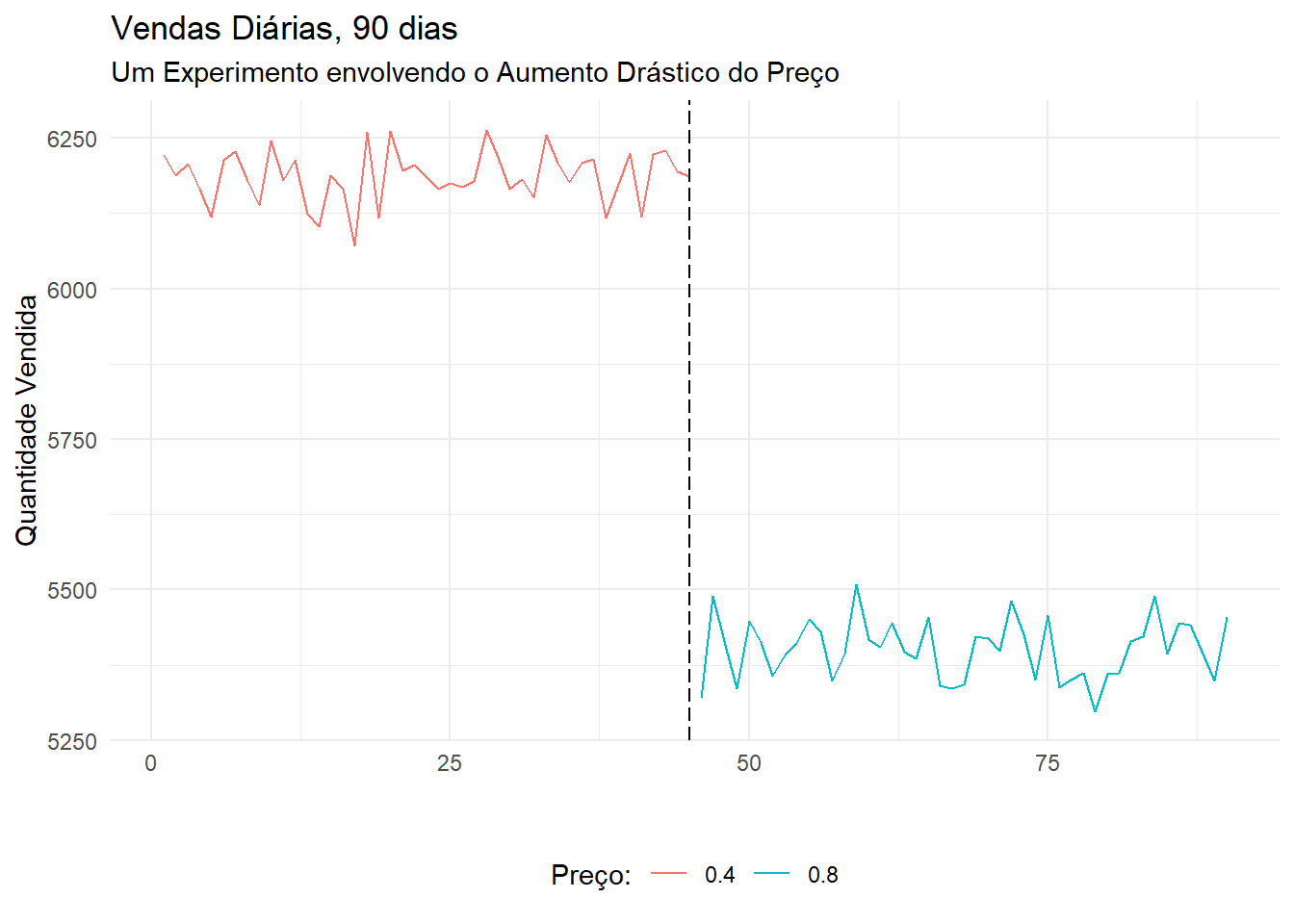
A figura mostra que a empresa executou um aumento brusco dos preços que os clientes que visitaram o site a partir de 46º dia se defrontaram. Agora podemos usar estes dados diários para estimar uma regressão linear do efeito do preço sobre a quantidade. A equação que vamos estimar está na forma:
\[Q = \beta_0 + \beta_1 P + \epsilon\]
Onde \(\beta_0\) tenta capturar o intercepto da curva de demanda e \(\beta_1\) estima a inclinação da reta de demanda, que é o nosso termo de interesse: \(\delta q / \delta p\).
modelo_reduzido <- df_diario %>%
# lm() estima um modelo de regressão linear
lm(quantidade ~ precos, .)
modelo_reduzido %>%
summary() %>%
broom::tidy() %>%
kableExtra::kable()| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | 6971.156 | 15.79844 | 441.25601 | 0 |
| precos | -1962.444 | 24.97952 | -78.56213 | 0 |
Segundo as estimativas acima, se o preço subisse \(\$1\), a quantidade vendida cairia em cerca de 1962 unidades. Como nosso preço foi elevado em \(\$ 0,4\), esperamos que as vendas médias diminuam em média 785 unidades.
Para ver este resultado em termos de elasticidade, só precisamos aplicar a fórmula de elasticidade utilizando o valor de \(\beta_1\), de \(p\) (que podemos utilizar o preço médio de \(\$ 0.6\)) e \(q\) (a quantidade média). Lembre que esta é uma aproximação da elasticidade para esta vizinhança de preços. Para valores mais distantes, podemos ter outros valores.
df_diario %>%
summarise(p = mean(precos),
q = mean(quantidade)) %>%
mutate(dqdp = modelo_reduzido$coefficients[2]) %>%
# elasticidade
mutate(elasticidade = dqdp*p/q) %>%
kableExtra::kable()| p | q | dqdp | elasticidade |
|---|---|---|---|
| 0.6 | 5793.689 | -1962.444 | -0.2032326 |
Assim, a elasticidade encontrada é de \(\frac{\Delta \% Q}{\Delta \% P} = -\frac{0.2}{1}\), de modo que um aumento de preço de 10% reduz a quantidade vendida do produto em apenas 2%. Nosso produto possui uma demanda inelástica neste ponto.
A partir dessas informações, podemos construir nossa curva de demanda e extrapolar nossos resultados para além dos preços de \(\$0.4\) e \(\$0.8\). Vamos assumir aqui um intervalo razoável entre \(\$ 0\) e \(\$ 3\) e calcular a quantidade vendida como \(6947, 13 - 1917,5P\).
intervalo_precos <- seq(0, 3, 0.01)
beta0 <- modelo_reduzido$coefficients[1]
beta1 <- modelo_reduzido$coefficients[2]
curva_demanda <- data.frame(precos = intervalo_precos) %>%
mutate(quantidade = (beta0 + beta1 * precos))
curva_demanda %>%
ggplot(aes(x = quantidade, y = precos)) +
geom_hline(yintercept = c(0.4, 0.8), linetype = 'longdash', color = "#2A73CC") +
geom_line(size = 1, color = "#FC4E07") +
labs(x = "Quantidade", y = "Preço", title = "Curva de Demanda Estimada") +
theme_minimal() 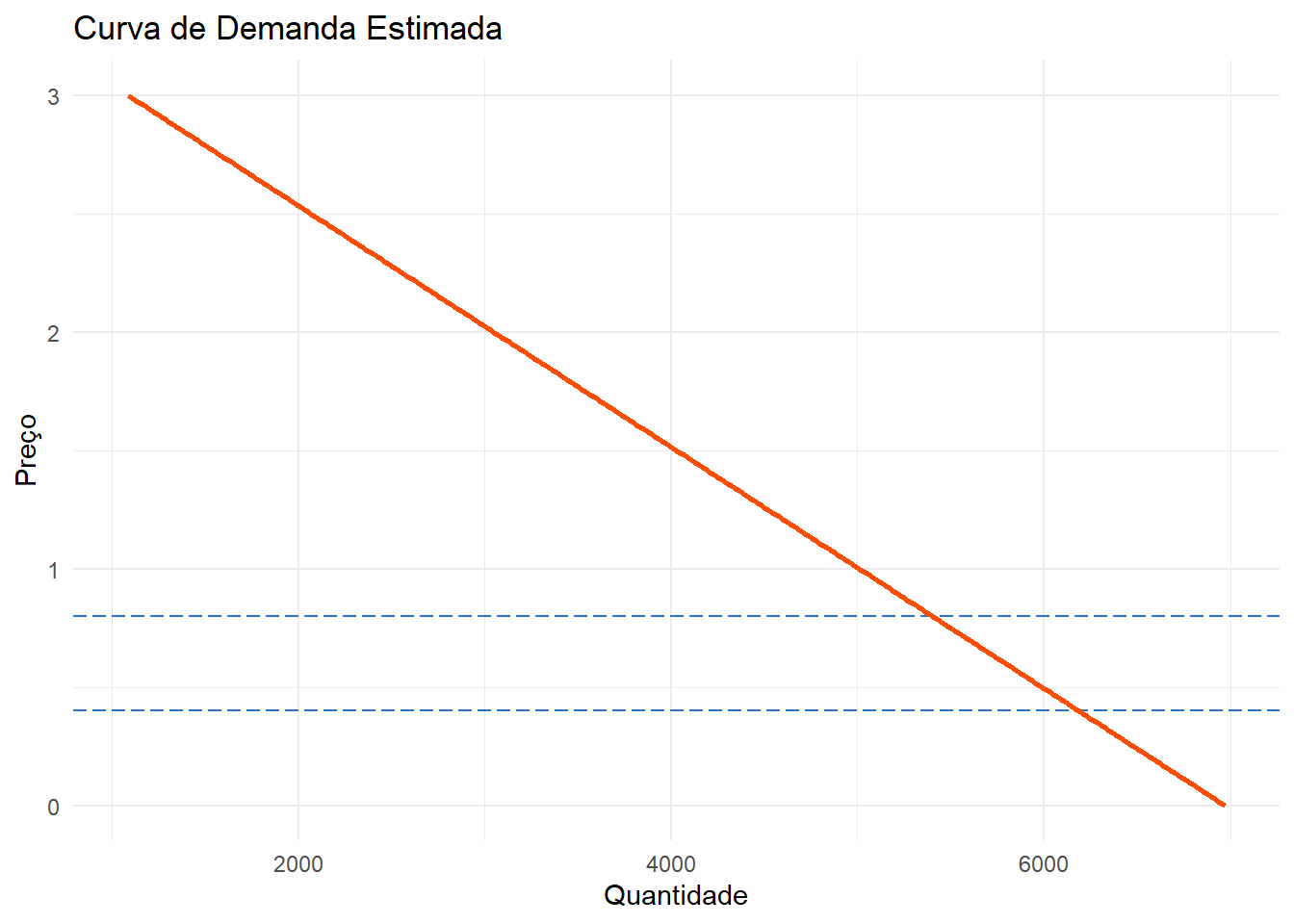
Assim, se a empresa resolvesse elevar o preço para \(\$ 1\), ela veria suas vendas cairem para cerca de 4500 unidades por dia, ou \(4500 \times 90 = 405000\) unidades ao longo de 90 dias.
Isto não significa que o lucro vai diminuir com a redução da quantidade. Se a demanda for pouco sensível a aumentos de preços, o efeito do aumento de preço pode dominar o efeito negativo da queda das vendas, produzindo um aumento de lucros. Para avaliar este efeito da mudança de preço sobre a receita, podemos derivar a curva de receitas a partir da curva de demanda. Como nossos custos são constantes, as mesmas conclusões são feitas para o lucro.
curva_receita <- curva_demanda %>%
mutate(quantidade_total = n * quantidade) %>%
mutate(receita = quantidade_total * precos)
preco_receita_max <- curva_receita %>%
filter(receita == max(receita)) %>%
pull(precos)
curva_receita %>%
mutate(lucro_max = max(receita)) %>%
ggplot(aes(x = precos, y = receita)) +
geom_line(size = 1, color = "#FC4E07") +
geom_vline(xintercept = c(0.4, 0.8), linetype = 'longdash', color = "#2A73CC") +
geom_vline(xintercept = preco_receita_max, linetype = "longdash") +
labs(x = "Preço", y = "Lucro", title = "Função de Receita Estimada", subtitle = "A Empresa poderia aumentar sua receita elevando o preço para $ 1.78") +
theme_minimal() 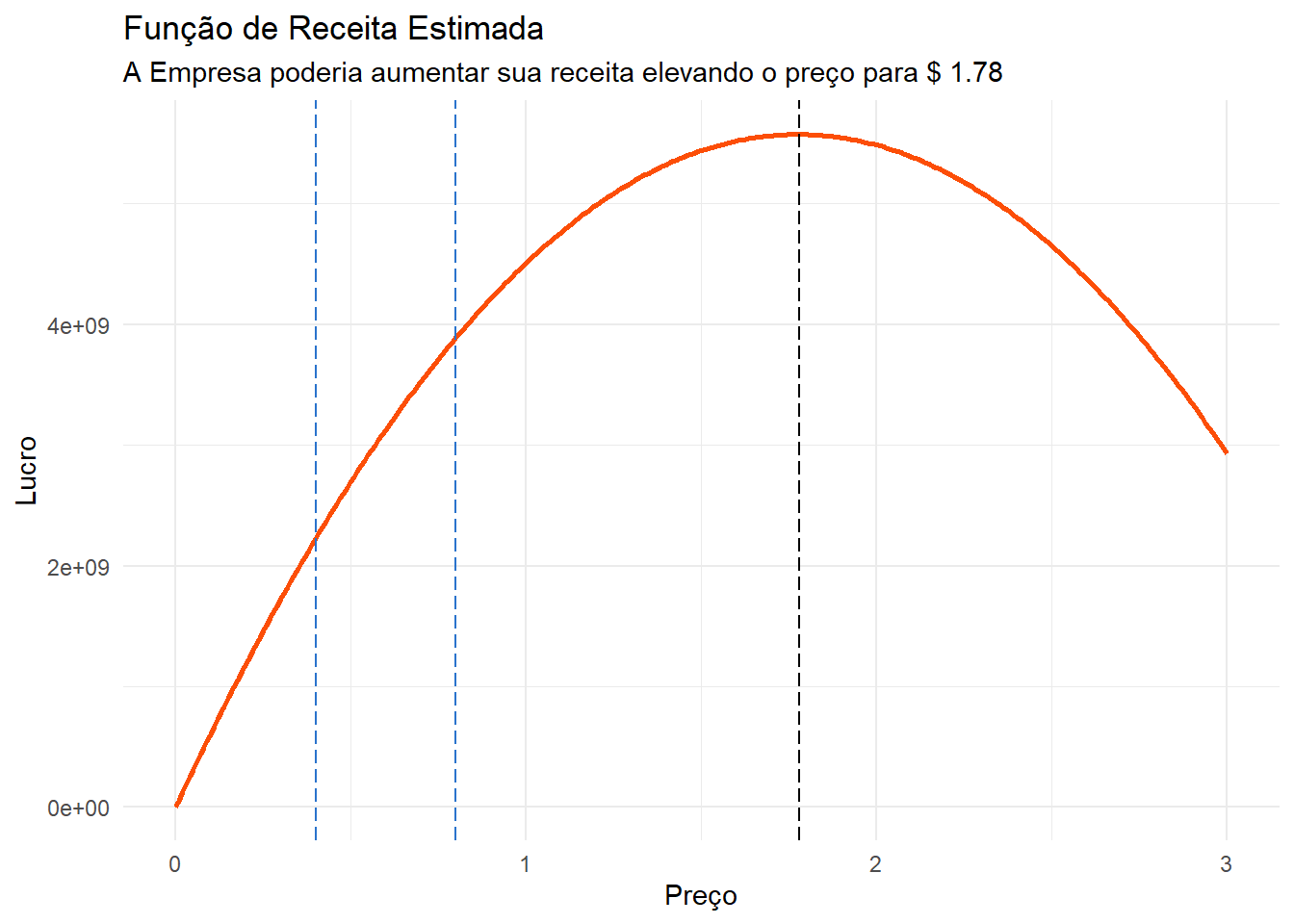
Assim, assumindo que nossa curva de receita está bem especificada, a firma poderia maximizar sua receita (e lucros) caso definisse um preço de \(\$ 1,78\). Considerando que o produto é bastante inelástico (\(\epsilon = -0.2\)), o efeito sobre a receita de um aumento de preço é positivo para esta faixa de preço, dado que o efeito do aumento do preço domina o efeito da queda das vendas.
\[\Delta \% RT = \Delta \%P + \Delta\%Q\]
Complicações com Dados Reais
Mas estas estimativas estão corretas? Para o nosso caso acima, sim. Como nosso banco de dados é sintético, ele foi construído de modo que a decisão de compra de um usuário dependa exclusivamente das suas preferências e do preço atual do produto.
Na prática as coisas podem ser mais complicadas. Mudanças de preços não ocorrem de maneira aleatória, mas geralmente são uma resposta à mudanças nas condições de mercado, assim como promoções são executadas numa tentativa de aumentar as vendas em um período de baixa procura. Existem ainda motivos que podem mudar a quantidade demanda e que nada tem a ver com mudanças de preços. Isso significa que é bem mais complicado isolar o efeito do preço sobre a quantidade.
A figura abaixo ilustra um aumento das vendas como resposta de um deslocamento da curva de demanda. O que pode ter promovido este deslocamento? Uma campanha de marketing bem executada, que aumentou a atratividade do produto, mesmo que o preço não tenha diminuido; ou a chegada de um feriado ou de uma época do ano que promova mais vendas.
plot_labels <- data.frame(label = c("S", "D[1]", "D[2]"), x = c(8, 9, 9),
y = c(90, 5, 20))
d_1 <- function(q) (q - 10)^2; d_2 <- function(q) (q - 10)^2 + 10
s_1 <- function(q) q^2 + 2*q + 20
x_range <- 0:5
curve_intersection <- curve_intersect(d_1, s_1, empirical = FALSE,
domain = c(min(x_range), max(x_range)))
new_curve_intersection <- curve_intersect(d_2, s_1, empirical = FALSE,
domain = c(min(x_range), max(x_range)))
ggplot() +
stat_function(aes(x_range), color = "#2A73CC", size = 1, linetype = "dashed",
fun = d_1, data = data.frame()) +
stat_function(aes(x_range), color = "#2A73CC", size = 1, fun = d_2, data = data.frame()) +
stat_function(aes(x_range), color = "#FC4E07", size = 1, fun = s_1, data = data.frame()) +
geom_vline(xintercept = curve_intersection$x, linetype = "dotted") +
geom_hline(yintercept = curve_intersection$y, linetype = "dotted") +
geom_vline(xintercept = new_curve_intersection$x, linetype = "dotted") +
geom_hline(yintercept = new_curve_intersection$y, linetype = "dotted") +
annotate("segment", x = 2.3, xend = 2.7, y = 60, yend = 62,
arrow = arrow(length = unit(0.3, "lines")), colour = "grey50") +
geom_text(data = plot_labels,
aes(x = x, y = y, label = label), parse = TRUE) +
labs(x = "Quantidade", y = "Preço",
title = "Deslocamento para a direita da demanda",
subtitle = "A Quantidade vendida pode aumentar por fatores que deslocam a curva") +
theme_classic()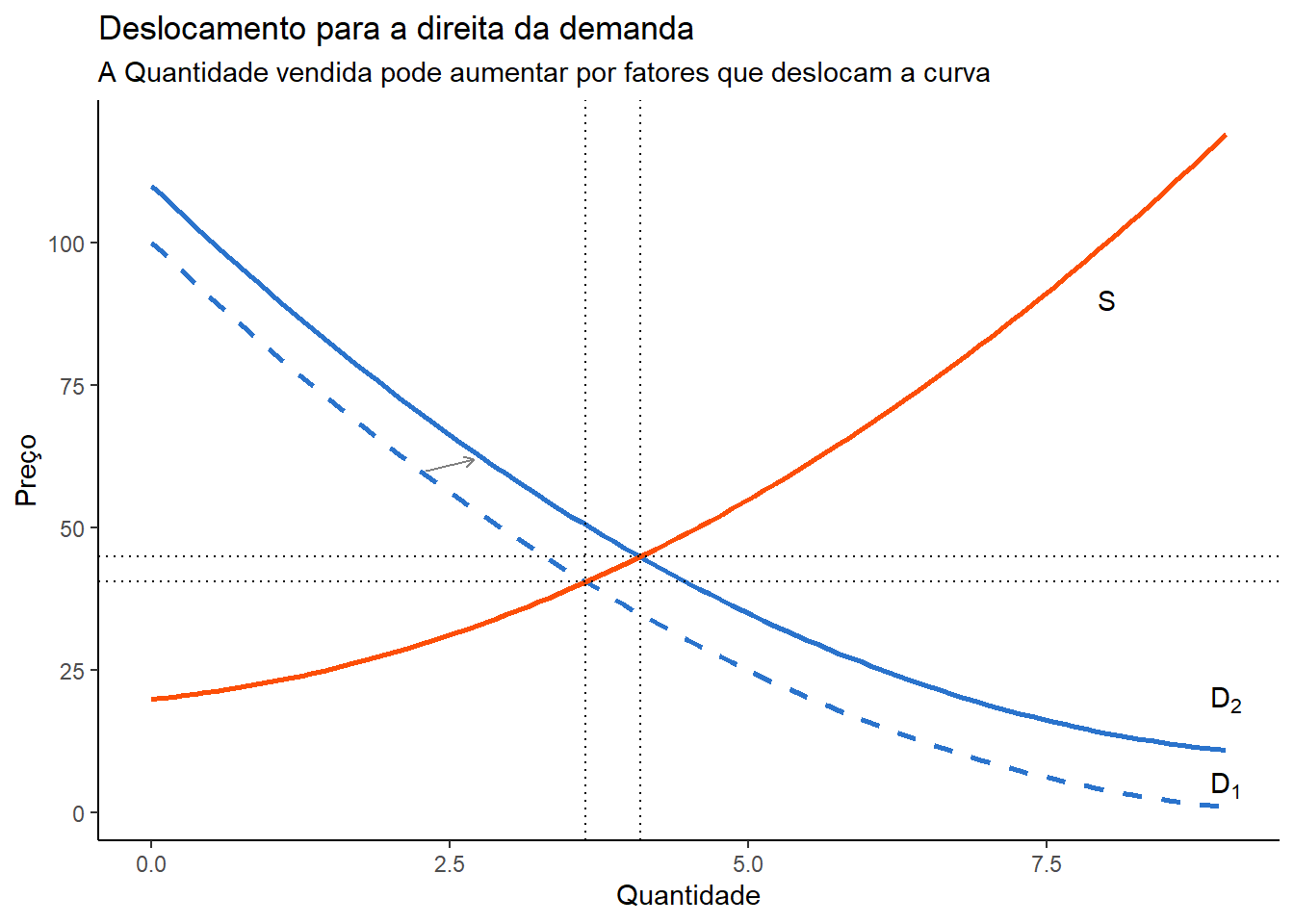
Assim, se houver um aumento de preço que coincida com o deslocamento da curva de demanda, ao estimar a relação entre preço e quantidade \(\frac{\delta q}{\delta p}\) como fizemos lá em cima, o coeficiente encontrado pode refletir estes outros eventos. Em um caso extremo, podemos estimar até mesmo um coeficiente positivo. Desse modo, não estaremos mais recuperando um coeficiente com interpretação causal, já que o efeito do preço está sendo confundida com o efeito de outros fatores que deslocaram a curva de demanda.
Para ilustrar esta situação, imagine que a decisão de compra permaneça a mesma. Ela depende (1) da utilidade média, que reflete a qualidade do produto e é igual para todos os consumidores, (2) da utilidade atribuída por cada consumidor e (3) do preço do produto. No primeiro exemplo, a empresa promoveu um aumento de preço em um dado ponto no tempo. Vamos permitir agora que a cada dia, o preço que os clientes se defrontam seja um pouco maior. Além disto, vamos assumir que a qualidade do produto varie no tempo. Assim, a cada 9 dias, a qualidade média do produto se altera. Se nosso produto fosse um curso online, um incremento da qualidade poderia representar um módulo a mais na ementa do curso, por exemplo.
# incremento nos precos de 0.4 para 1.8 a cada 1 dia. Totalizando 90 incrementos.
precos <- seq(from = 0.4, to = 1.8, length.out = 90) %>%
rep(n / 90) %>%
sort()
# incremento na qualidade media a cada 9 dias. Totalizando 10 incrementos.
utilidade_media <- seq(from = 0.1, to = 0.9, length.out = 10) %>%
rep(n / 10) %>%
sort()
df_diario_2 <- data.frame(dia = dia,
componente_usuario = rnorm(n = n)) %>%
mutate(precos = precos,
utilidade_media = utilidade_media,
utilidade_produto = utilidade_media + componente_usuario +
coef_preco * precos,
comprou = (utilidade_produto > 0)) %>%
group_by(dia) %>%
summarise(quantidade = sum(comprou),
precos = max(precos),
qualidade = max(utilidade_media))
df_diario_2 %>%
ggplot(aes(x = dia, quantidade)) +
geom_line() +
geom_line(aes(color = as.factor(qualidade %>% round(1)))) +
labs(x = "", y = "Quantidade Vendida",
color = "Qualidade:", title = "Vendas Diárias, 90 dias",
subtitle = "Aumento na quantidade reflete mudança de preço e de qualidade") +
theme_minimal() +
theme(legend.position = 'bottom')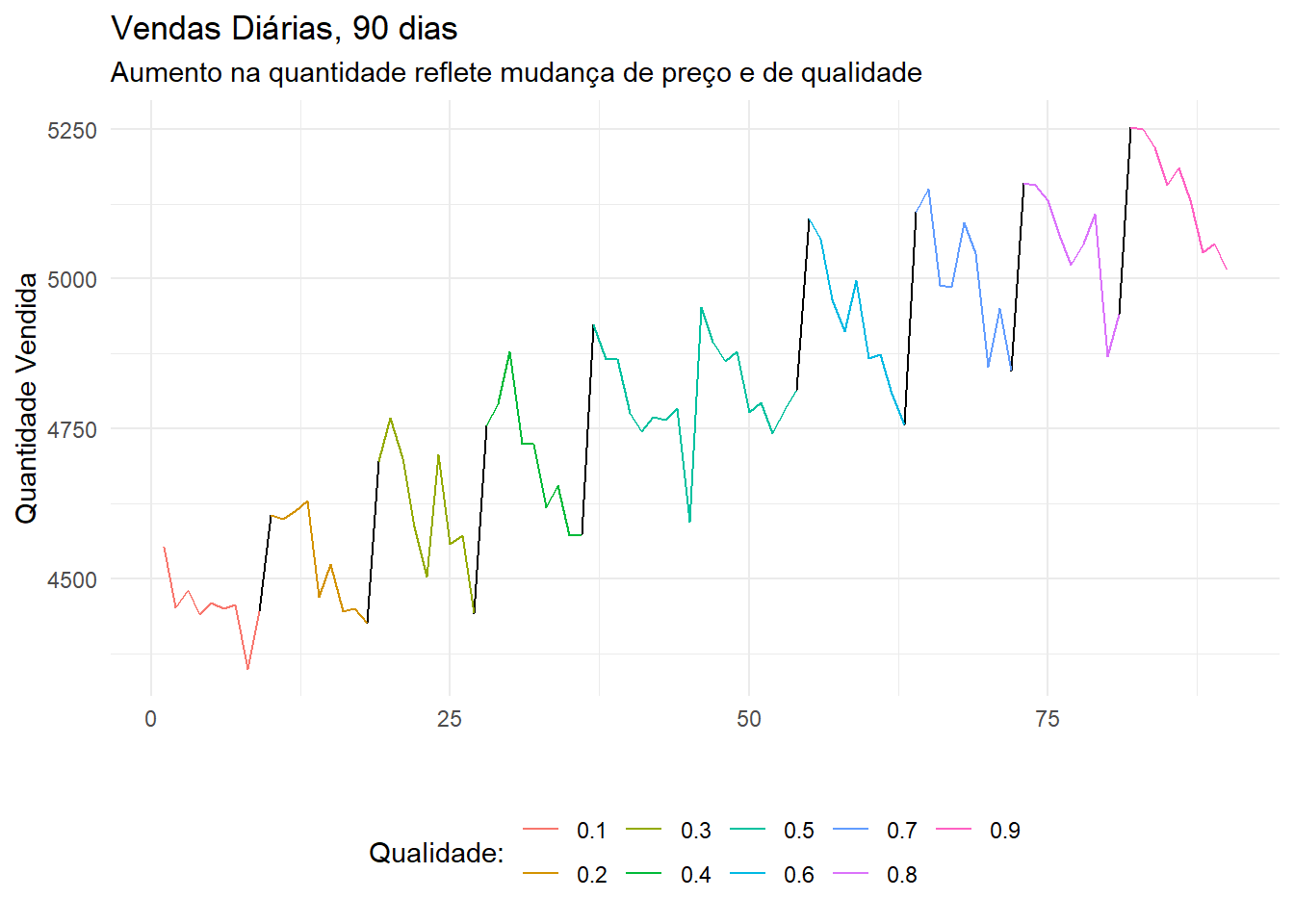
O gráfico acima mostra que a quantidade vendida ao longo do período aumentou, a despeito do aumento de preço que ocorreu no período (de \(\$ 0.4\) para \(\$ 1.8\)). É bastante improvável que a quantidade vendida aumente como resposta a aumentos de preços (a exceção são os bens de Gifen). O mais provável é que o efeito do preço esteja sendo confudido pelo aumento na qualidade do produto. A qualidade promove um aumento na quantidade vendida, mas o aumento dos preços desestimula parte dos consumidores. O efeito líquido é positivo, pois o aumento na qualidade mais que compensa os produtos mais caros.
Neste tipo de situação, ao estimarmos o efeito dos preços sobre a quantidade vendida, o coeficiente para o preço (\(\frac{\delta q}{\delta p}\)) obtido pela regressão linear será positivo. Assim, aquilo que a regressão nos informa é muito diferente daquilo que desejamos. O que queremos é o efeito dos preços sobre a quantidade vendida, ceteris paribus, que significa que desejamos manter constantes todos os outros fatores que impactam a quantidade, e assim obter exclusivamente o efeito dos preços.
df_diario_2 %>%
# lm() estima um modelo de regressão linear
lm(quantidade ~ precos, .) %>%
summary() %>%
broom::tidy() %>%
kableExtra::kable()| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | 4237.1117 | 32.90698 | 128.76026 | 0 |
| precos | 516.3025 | 28.04274 | 18.41127 | 0 |
Para nosso exemplo, o novo \(\beta_1\) é positivo e igual a \(\beta_1 = 471\), um resultado nada razoável.
Técnicas de Inferência Causal
Quando movimentos em outras variáveis confundem o efeito do preço sobre a quantidade, a correlação entre preço e quantidade não tem nenhuma interpretação causal. Para garantir que nossos resultados representam o efeito de \(X\) em \(Y\) podemos fazer uso de experimentos aleatorizados.
Um método comum de experimentos aleatórios é o chamado teste AB, em que um conjunto de usuários é aleatoriamente escolhido para participar de um grupo de tratamento, onde alguma intervenção é realizada. Por outro lado, um outro conjunto de usuários são atribuidos aleatoriamente a um grupo de controle. A importância dos dois grupos está na possibilidade de realizar comparações entre um grupo de indivíduos que sofreu um tratamento e outro que não.
Já a atribuição aleatória garante que estamos eliminando a possibilidade de que fatores confundidores estejam prejudicando nossas estimativas da intervenção sobre a nossa métrica de interesse. Por exemplo, ao incluir uma característica nova ao nosso site fictício, podemos estar interessados em aumentar o engajamento dos usuários. Para testar o efeito desta mudança sobre nossa métrica, podemos permitir que apenas um sub-conjunto de usuários interaja com o novo site. Mas como esses usuários são escolhidos para o tratamento? poderiamos incluir um botão que leva o cliente para o novo site. Mas este modelo de seleção poderia viesar nossas estimativas do efeito da mudança sobre o engajamento, dado que usuários mais curiosos podem ser naturalmente mais engajados. O efeito da mudança no site sobre o engajamento pareceria maior do que realmente é.
Assim, o processo aleatório elimina o problema de viés de seleção, e garante que os indivíduos tratados e não tratados venham da mesma população e sejam estatísticamente semelhantes em todas as suas características. A probabilidade de alguém que gosta muito do nosso produto estar no grupo de tratamento é muito parecida com a probabilidade de estar no grupo de controle. Da mesma forma, a proporção de clientes homens e mulheres deve refletir o que é observado na população, etc.
Em relação à experimentos envolvendo mudanças de preços, a empresa pode gerar mudanças de preço em ponto específico no tempo; pode testar diferenças de preços entre diferentes produtos; ou diferentes subgrupos de clientes. Estas são formas de testar o efeito de variação no preço sem se preocupar com o efeito de fatores confundidores.
Contudo, nem sempre experimentos são possíveis. Muitas vezes eles podem impactar negativamente a experiência dos clientes, já que ele pode representar um desvio da sua experiência habitual. Experimentos aleatorizados também podem ser caros de ser implementados. E em relação à experimentos envolvendo mudanças de preço, eles podem ser percebidos como anti-éticos pelos consumidores, podendo até mesmo produzir perda de confiança.
Regressão com Controles
Quando experimentos aleatorizados não são possíveis, o uso de dados históricos (chamados dados observacionais) podem ser utilizados para recuperar coeficientes causais utilizando algumas ferramentas, sob certas condições.
A ferramenta mais básica é o uso da regressão com controles. Com ela podemos realizar comparações envolvendo observações do tratamento e controle que possuam as mesmas características. No segundo caso, em que discutimos o efeito da qualidade e do preço sobre a quantidade vendida, podemos comparar os grupos de controle (preço menor) e de tratamento (preço maior) mantendo a qualidade do produto constante. Como são 10 níveis de qualidade (\(u_1, u_2, ..., u_10\)), devemos mensurar o efeito do aumento de preço dentro de cada categoria.
Para tanto, podemos realizar uma regressão para cada grupo de qualidade. Como temos 10 grupos, realizamos 10 regressões, com cada grupo tendo um nível de qualidade constante. A tabela abaixo mostra que para todos as 10 regressões, o efeito do preço é negativo, como esperado.
regressao_por_qualidade <- df_diario_2 %>%
group_by(qualidade) %>%
# nest permite criar 10 dataframes a partir da nossa base de dados.
nest() %>%
# aqui rodamos o modelo lm() e salvamos o resultado para cada grupo.
mutate(fit = map(data, ~lm(quantidade ~ precos, data = .)),
results = map(fit, broom::tidy)) %>%
unnest(results) %>%
filter(term == 'precos') %>%
select(-data, -fit, -term) %>%
rename(Efeito_Preco = estimate) %>%
ungroup() %>%
mutate_if(is.numeric, round, 2)
regressao_por_qualidade %>%
kableExtra::kable()| qualidade | Efeito_Preco | std.error | statistic | p.value |
|---|---|---|---|---|
| 0.10 | -825.37 | 335.89 | -2.46 | 0.04 |
| 0.19 | -1706.89 | 345.66 | -4.94 | 0.00 |
| 0.28 | -1872.18 | 634.29 | -2.95 | 0.02 |
| 0.37 | -2054.42 | 470.70 | -4.36 | 0.00 |
| 0.46 | -1875.36 | 422.33 | -4.44 | 0.00 |
| 0.54 | -1279.90 | 342.33 | -3.74 | 0.01 |
| 0.63 | -2523.79 | 329.76 | -7.65 | 0.00 |
| 0.72 | -1991.90 | 577.36 | -3.45 | 0.01 |
| 0.81 | -1897.61 | 485.31 | -3.91 | 0.01 |
| 0.90 | -2013.10 | 207.37 | -9.71 | 0.00 |
A forma de estimar acima é apenas ilustrativa. De modo muito mais simples, podemos realizar uma regressão linear que além de incluir o preço como um preditor, também inclui a variável qualidade. Como nossos dados foram construídos de modo sintético, temos a certeza de que apenas estes dois fatores influenciam a decisão de compra, de modo que uma regressão de quantidade com preços e qualidade como regressores consegue separar bem os efeitos do preço sobre a quantidade (\(\frac{\delta q}{\delta p}\)) do o efeito da qualidade sobre a quantidade (\(\frac{\delta q}{\delta u}\)).
df_diario_2 %>%
# lm() estima um modelo de regressão linear
lm(quantidade ~ precos + qualidade, .) %>%
summary() %>%
broom::tidy() %>%
kableExtra::kable()| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | 4923.257 | 42.49405 | 115.85754 | 0 |
| precos | -1804.051 | 134.25679 | -13.43732 | 0 |
| qualidade | 3732.488 | 214.89431 | 17.36895 | 0 |
A tabela acima mostra que o aumento de uma unidade monetária reduz a quantidade vendida em 1908 unidades, um resultado muito mais razoável.
Conclusão
Vimos que com o uso de dados históricos de preço e vendas podemos estimar o efeito do preço sobre a quantidade vendida. Por sua vez, esta medida pode ajudar uma empresa a decidir o preço ótimo de venda, que é aquele que maximiza receita.
Contudo, no mundo real, a quantidade vendida é o reflexo de muitos efeitos diferentes, e dificilmente vamos obter uma estimativa não viesada dos efeitos do preço sobre a quantidade se fizermos uma regressão simples com estas duas medidas. Da mesma forma, mudanças de preço raramente são eventos exógenos, mas refletem mudanças nas condições de mercado.
Para recuperar o efeito causal do preço sobre a quantidade, duas ferramentas simples podem ser utilizadas: experimentos aleatórios e regressão com controles. Experimentos aleatórios se bem conduzidos garantem que nossas estimativas estão livres do problema de autosseleção, de modo que as estimativas de preço sobre quantidade tem interpretação causal.
Quando experimentos aleatórios não são possíveis, a alternativa mais simples é o uso de regressão com controles. Nesta situação, as demais variáveis que ajudam a explicar a quantidade vendida entram na equação de regressão como regressores. Com isso esperamos comparar o grupo de tratamento (preço maior) com o grupo de controle (preço menor) quando ambos tem as mesmas características: qualidade do produto, campanha de marketing, sazonalidade, etc. Se nossos dados estiverem a nível de usuário, podemos ainda controlar para características pessoais de cada indivíduo.
Mas e quando não sabemos todas as variáveis relevantes? E quando as vendas dependem de fatores difíceis de mensurar, ou que são não observáveis? Temos um conjunto de ferramentas que podem ser utilizadas dentro do contexto de dados observacionais:
O método de Diferença-em-diferença pode ser utilizada quando temos grupos de controle e tratamento bem definidos, com observações antes e depois da intervenção.
Regressão com descontinuidade pode ser útil quando unidades são atribuidas ao grupo tratamento segundo algum critério bem definido.
Propensity-Score Matching (PSM) pode ser utilizado quando temos características dos indivíduos antes do tratamento, e assim podemos tentar tornar os dois grupos mais homogêneos.
Série temporal com interrupção podem ser utilizadas quando temos uma série temporal e um evento específico.
Controle sintético, que constroi um grupo de comparação a partir de uma média de diversas observações de controle.
Variáveis instrumentais, para os casos em que exista uma terceira variável, chamada de instrumento, que influencia a variável dependente através do tratamento.
Além disto, nem todos os experimentos aleatórios são iguais, e podemos utilizar diversos métodos de experimentos para resolver problemas que dependam de estimação causal:
CUPED/PSM para quando ainda existem diferenças importantes entre o grupo de tratamento e controle.
Complier Average Causal Effect (CACE) para quando algumas pessoas no grupo de tratamento acabaram não recebendo o tratamento.
Modelo Uplift e Efeito Tratamento Heterogêneo para quando o tratamento tem efeitos muito diferentes entre diferentes sub-grupos de consumidores.
Modelo de Mediação, caso seja interessante descobrir porque um tratamento alterou (ou não) nossa variável dependente.
Em uma postagem futura posso discutir alguns destes métodos.
Referências
[1] JOSHUA D. Angrist & PISCHKE, Jörn-Steffen. Mastering ’Metrics: The Path from Cause to Effect. Princeton University Press, 1ª Edição. 2014.
[2] SANDS, Emily Glassberg. How to Get the Price Right. Medium, 2016. Disponível em: https://medium.com/teconomics-blog/how-to-get-the-price-right-9fda84a33fe5. Acesso em 11 de Abril de 2021.
[3] HARINEN, Totte & LI, Bonnie. Using Causal Inferecent o Imrpove the Uber User Experience. Uber Enginneering, 2019. Disponível em: https://eng.uber.com/causal-inference-at-uber/. Acesso em 11 de Abril de 2021.