Estimando Crescimento com Função CES

Last updated on 4 de Apr de 2021 13 min read

Introdução

A especifição formal de uma função de produção CES com dois inputs é dada por

$y = γ (δ x_{1}^{- ρ} + (1 - δ) x_{2}^{- ρ})^{- \frac{ν}{ρ}}$

onde $y$ é a quantidade de produto, $x_{1}$ e $x_{2}$ são os input, e $γ$ , $δ$ e $ν$ são parâmetros. O parâmetro $γ \in [0, \infty)$ determina a produtividade, $δ \in [0, 1]$ determina a distribuição ótima dos input, $ρ \in [- 1, 0) \cup (0, \infty)$ , a elasticidade (constante) de substituição, que é igual a $σ = 1 / (1 + ρ)$ , e $ν \in [0, \infty)$ é igual a elasticidade de escala ¹.

A função CES inclui três casos especiais:

$ρ \to 0$ , $σ$ se aproxima de 1 e a CES toma a forma de uma Cobb Douglas;
$ρ \to \infty$ produz $σ \to 0$ e a CES se torna uma Leontief; e
$ρ \to - 1$ produz $$ e a CES se torna uma fun??o linear se $ν = 1$ .

Os dois procedimentos padrões para estimar os parâmetros das funções CES são a aproximação de Taylor desenvolvida por Kmenta (1967) e a estimação de Mínimos quadrados não lineares (NLS). Contudo, a aplicação da aproximação de Kmenta é limitada, porque ela não pode ser usada para funções CES com mais que dois inputs (Hoff, 2004), portanto só retornando resultados confiáveis se $ρ$ está próximo de zero. Ao mesmo tempo, algorítmos de aproximação não linear quase sempre se defrontam com problemas de convergência.

Ferramentas para análise econômica com a função CES estão disponíveis no pacote R micEconCES

Podemos demonstrar a estimação de uma função CES com dois inputs, bem como uma nested CES com três ou quatro inputs. Criando um banco de dados com quatro inputs e então criando um a função cesCalc para calcular o output determinístico para uma CES com dois inputs e com especificação $γ = 1$ , $δ = 0.6$ , $ρ = 0.5$ e $ν = 1.1$ . Por fim, a última linha de comando produz a variável output estocástica adicionando erros normalmente distribuidos para a variável output deteminística.

library(micEconCES)
library(tidyverse)

set.seed(123)
cesData <- data.frame(x1 = rchisq(200, 10), 
                      x2 = rchisq(200, 10),
                      x3 = rchisq(200, 10),
                      x4 = rchisq(200, 10))

cesData <- cesData %>% 
  mutate(y2 = cesCalc(xNames = c( "x1", "x2" ), data = cesData,
                      coef = c(gamma = 1, delta = 0.6, rho =0.5, nu = 1.1)
                      )) %>% 
  mutate(y2 = y2 + 2.5*rnorm(200))

cesData %>% head()

##          x1        x2        x3        x4        y2
## 1  6.779170  8.628172  9.466569 14.289714  6.537563
## 2 14.757915  7.912423  4.859748  2.691979 15.820243
## 3  3.259122  8.524324  5.129477 23.531115  5.058388
## 4  9.556879 13.206816  8.451157 21.763253 13.062918
## 5 17.747128  7.591901  8.546469 10.469937 16.672353
## 6 11.061724  9.201171 20.834041  8.290596 10.392037

Podemos realizar o mesmo procedimento para uma função com três e quatro inputs:

cesData <- cesData %>% 
  mutate(y3 = cesCalc(xNames = c("x1", "x2", "x3"), data = cesData,
                      coef = c( gamma = 1, delta_1 = 0.7, 
                                delta = 0.6, rho_1 = 0.3, 
                                rho = 0.5,nu = 1.1), nested = TRUE )) %>% 
  mutate(y3 = y3 + 1.5*rnorm(200))


cesData <- cesData %>% 
  mutate(y4 = cesCalc(xNames = c("x1", "x2", "x3", "x4"), data = cesData,
                      coef = c(gamma = 1, delta_1 = 0.7, 
                               delta_2 = 0.6, delta = 0.5,
                               rho_1 = 0.3, rho_2 = 0.4, 
                               rho = 0.5, nu = 1.1), 
                      nested = TRUE)) %>% 
  mutate(y4 = y4 + 1.5*rnorm(200))

cesData %>% head()

##          x1        x2        x3        x4        y2        y3        y4
## 1  6.779170  8.628172  9.466569 14.289714  6.537563  8.827164 11.032190
## 2 14.757915  7.912423  4.859748  2.691979 15.820243 11.029816  9.515718
## 3  3.259122  8.524324  5.129477 23.531115  5.058388  7.441439  5.979330
## 4  9.556879 13.206816  8.451157 21.763253 13.062918 10.856928 15.007432
## 5 17.747128  7.591901  8.546469 10.469937 16.672353 13.105363 14.566526
## 6 11.061724  9.201171 20.834041  8.290596 10.392037 18.345526 13.565679

Como a CES é não linear nos seus parâmetros, a forma mais direta de estimar a função CES no R seria usando a função nls, que estima mínimos quadrados não lineares:

cesNls <- cesNls <- nls(y2 ~ gamma*(delta*x1^(-rho) + (1-delta)*x2^(-rho))^(-phi/rho),
                        data = cesData, start = c(gamma = 0.5, delta = 0.5, rho = 0.25, phi=1))
print(cesNls)

## Nonlinear regression model
##   model: y2 ~ gamma * (delta * x1^(-rho) + (1 - delta) * x2^(-rho))^(-phi/rho)
##    data: cesData
##  gamma  delta    rho    phi 
## 1.0239 0.6222 0.5420 1.0858 
##  residual sum-of-squares: 1197
## 
## Number of iterations to convergence: 6 
## Achieved convergence tolerance: 8.194e-06

Enquanto nls funciona bem em exemplos artificiais, ela não é capazes de produzir bons resultados com dados reais, seja por problemas de não-convergência, de convergência para mínimo local ou por estimativa de parâmetros teoricamente pouco razoáveis. Portanto, é preciso encontrar formas alternativas de estimação.

Aproximação Kmenta

Aproximação de Kmenta produz uma linearidade que permite a estimação da CES por MQO:

$\ln y = \ln γ + ν δ \ln x_{1} + ν (1 - δ) \ln x_{2} - \frac{ρ ν}{2} δ (1 - δ) (\ln x_{1} - \ln x_{2})^{2}$

Kmenta obteve esta fórmula logaritmizando a função CES e aplicando a expansão de Taylor de segunda ordem para $\ln (δ x_{1}^{- ρ} + (1 - δ) x_{2}^{- ρ})$ no ponto $ρ = 0$ . A mesma fórmula pode ser obtida aplicando a expansão de Taylor de primeira ordem para toda a função CES logaritmizada no ponto $ρ = 0$ (Uebe 2000).

A Aproximação de Kmenta pode ser escrita como uma função translog restrita (Hoff 2004):

$\ln y = α_{0} + α_{1} \ln x_{1} + α_{2} \ln x_{2}$ $+ \frac{1}{2} β_{11} (\ln x_{1})^{2} + \frac{1}{2} β_{22} (\ln x_{2})^{2} + β_{12} \ln x_{1} \ln x_{2}$

onde as restrições são que $β_{12} = - β_{11} = - β_{22}$ . Se retornos constantes de escala são impostos, uma terceira restrição deve ser aplicada $α_{1} + α_{2} = 1$ .

Essas restrições podem ser utilizadas para testar se a aproximação de Kmenta é uma simplifição aceitável da forma funcional translog. Neste caso, um simples teste t para os coeficientes pode ser usado para checar se a forma funcional Cobb-Douglas é uma simplificação aceitável da aproximação Kmenta da CES.

Os parámetros da função CES podem ser calculados a partir de parâmetros da translog restrita por:

$γ = \exp (α_{0})$

$ν = α_{1} + α_{2}$

$δ = \frac{α_{1}}{α_{1} + α_{2}}$

$ρ = \frac{β_{12} (α_{1} + α_{2})}{α_{1} α_{2}}$

A aproximação de Kmenta pode ser estimada usando a função cesEst.

cesKmenta <- cesEst(yName = "y2", xNames = c("x1","x2"), data = cesData, method = "Kmenta", vrs = TRUE)

## Warning in log(data[[varNames[i]]]): NaNs produzidos

## Warning in estData$y - result$residuals: comprimento do objeto maior não é
## múltiplo do comprimento do objeto menor

summary(cesKmenta)

## Estimated CES function with variable returns to scale
## 
## Call:
## cesEst(yName = "y2", xNames = c("x1", "x2"), data = cesData, 
##     vrs = TRUE, method = "Kmenta")
## 
## Estimation by the linear Kmenta approximation
## Test of the null hypothesis that the restrictions of the Translog
## function required by the Kmenta approximation are true:
## P-value = 0.2269042
## 
## Coefficients:
##       Estimate Std. Error t value Pr(>|t|)    
## gamma  0.89834    0.14738   6.095 1.09e-09 ***
## delta  0.68126    0.04029  16.910  < 2e-16 ***
## rho    0.86321    0.41286   2.091   0.0365 *  
## nu     1.13442    0.07308  15.523  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 2.498807 
## Multiple R-squared: 0.7548401 
## 
## Elasticity of Substitution:
##             Estimate Std. Error t value Pr(>|t|)    
## E_1_2 (all)   0.5367     0.1189   4.513 6.39e-06 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

O teste de Walk indica que as restrições na função translog implicadas pela apoximação de Kmenta não podem ser rejeitadas. Podemos ver se a tecnologia não tem forma Cobb Douglas, para isso checamos se $β_{12} = - β_{22} = - β_{11}$ são significante diferentes de zero. Como a estimação da aproximação de Kmenta está no componente cesEst$kmenta, podemos observa-los como

cesKmenta %>% {.$kmenta} %>% summary() %>% coef()

##                   Estimate Std. Error    t value     Pr(>|t|)
## eq1_(Intercept) -0.1072116 0.16406442 -0.6534723 5.142216e-01
## eq1_a_1          0.7728315 0.05785460 13.3581693 0.000000e+00
## eq1_a_2          0.3615885 0.05658941  6.3896839 1.195467e-09
## eq1_b_1_1       -0.2126387 0.09627881 -2.2085723 2.836951e-02
## eq1_b_1_2        0.2126387 0.09627881  2.2085723 2.836951e-02
## eq1_b_2_2       -0.2126387 0.09627881 -2.2085723 2.836951e-02

Dado que $β_{12} = - β_{22} = - β_{11}$ diferem significatiamente de zero ao nível de 5%, podemos concluir que a tecnologia não é da forma Cobb Douglas. Alternativamente podemos chegar se o parâmetro $ρ$ da função CES é significativamente diferente de zero. Que produz resultados semelhantes.

Finalmente, plotando os valores ajustados contra os valores observados de $y$ para checar se os parâmetros são razoáveis:

cesData %>% 
  ggplot(aes(x = y2, y = fitted(cesKmenta))) + 
  geom_point() + 
  theme_bw()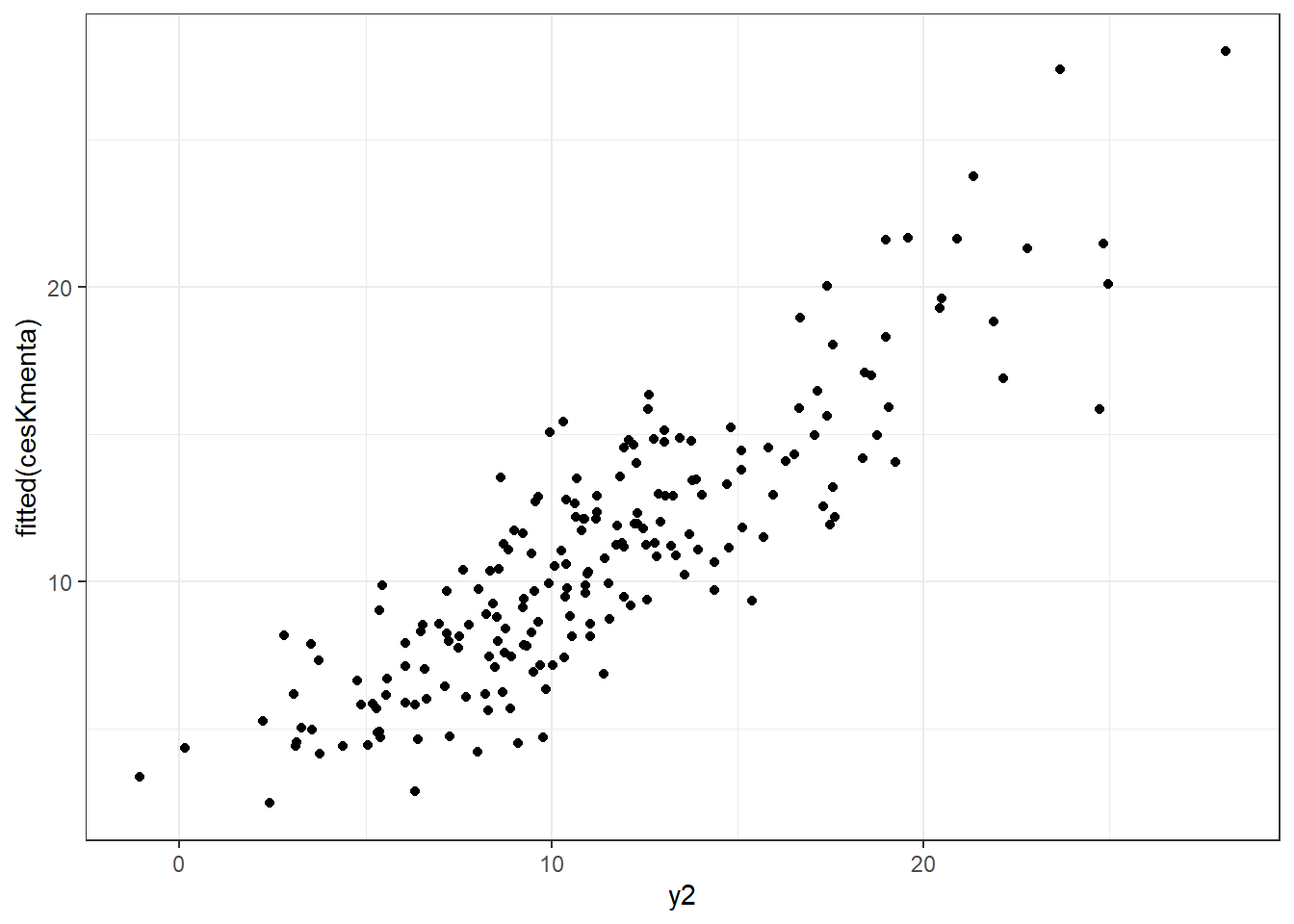

Figura acima mostra que os parâmetros produzem valores ajustados razoáveis. Porém, a aproximação de Kmenta produz vários problemas. Primeiro, ela é uma série de Taylor truncada e o termo Resto deve ser visto como uma variável omitida. Segundo, a aproximação de Kmenta apenas converge para a função CES na região de convergência que é dependente do verdadeiro parâmetro da CES (Thursby and Lovell 1978).

Replicação de Sun, Henderson and Kumbhakar (2011)

O estudo é uma replicação de Masanjala and Papagergious (2004). O objetivo é reeestimar um modelo de Solow baseado na função CES com capital e trabalho aumentado (i.e., a quantidade de trabalho multiplicada pela eficiência do trabalho) como inputs. O modelo é dado como:

$y_{i} = A {[\frac{1}{1 - α} - \frac{α}{1 - α} {(\frac{s_{i k}}{n_{i} + g + δ})}^{\frac{σ - 1}{σ}}]}^{- \frac{σ}{σ - 1}}$

onde

$y_{i}$ é o produto de estado estacionário (PIB) por unidade de trabalho.
$s_{i k}$ ? a razáo de investimento por produto agregado.
$n_{i}$ ? a taxa de crescimento da população com o subscrito $i$ indicando a população.
$g$ é a taxa de crescimento tecnologica.
$δ$ ? a taxa de depreciação do capital.

$A$ indica a eficiência do trabalho.

$α$ é o parâmetro de distribuição do capital.

$σ$ é a elasticidade de substituição.

Podemos redefinir os parâmetros e variáveis na função acima para obter a CES com dois inputs: $γ = A$ , $δ = \frac{1}{1 - α}$ , $x_{1} = 1$ , $x_{@} = (n_{i} + g + δ) / s_{i k}$ , $ρ = (σ - 1) / σ$ e $ν = 1$ . Neste caso, a elasticidade é um pouco diferente do modelo CES padrão, com elasticidade de substituição dada por $σ = 1 / (1 - ρ)$ (assim, o $ρ$ possui sinal inverso). Portanto, o $ρ$ estimado deve estar entre menos infinito e um. Além disso, $α$ deve estar entre zero e um, de modo que $δ$ estimado tenha valor maior que um ou igual a um.

Os dados utilizados são aqueles de Mankiw, Romer e Weil (1992) e não inclui os países produtores de petróleo.

data("GrowthDJ", package = "AER")
GrowthDJ <- GrowthDJ %>% 
  filter(oil == "no")
GrowthDJ %>% head()

##   oil inter oecd gdp60 gdp85 gdpgrowth popgrowth invest school literacy60
## 1  no   yes   no  2485  4371       4.8       2.6   24.1    4.5         10
## 2  no    no   no  1588  1171       0.8       2.1    5.8    1.8          5
## 3  no    no   no  1116  1071       2.2       2.4   10.8    1.8          5
## 4  no   yes   no   959  3671       8.6       3.2   28.3    2.9         NA
## 5  no    no   no   529   857       2.9       0.9   12.7    0.4          2
## 6  no    no   no   755   663       1.2       1.7    5.1    0.4         14

Podemos calcular os dois inputs do modelo (seguindo a suposição de Mankiw de que $g + δ = 0, 05$ :

GrowthDJ <- GrowthDJ %>% 
  mutate(x1 = 1,
         x2 = (GrowthDJ$popgrowth + 5) / GrowthDJ$invest)

Estimador em Nível: NLS

O modelo a seguir estima o modelo de Solow em uma função CES usando NLS:

cesNls <- cesEst("gdp85", c("x1", "x2"), data = GrowthDJ)
summary(cesNls, ela = FALSE)

## Estimated CES function with constant returns to scale
## 
## Call:
## cesEst(yName = "gdp85", xNames = c("x1", "x2"), data = GrowthDJ)
## 
## Estimation by non-linear least-squares using the 'LM' optimizer
## assuming an additive error term
## Convergence achieved after 23 iterations
## Message: Relative error in the sum of squares is at most `ftol'. 
## 
## Coefficients:
##       Estimate Std. Error t value Pr(>|t|)  
## gamma  646.141    549.993   1.175   0.2401  
## delta    3.977      2.239   1.776   0.0757 .
## rho     -0.197      0.166  -1.187   0.2354  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 3313.748 
## Multiple R-squared: 0.6016277

Agora, podemos calcular o parámetro de distribuição do capital ( $α$ ) e a elasticidade de substituição ( $σ$ ) manualmente:

cat("alpha =", (coef(cesNls)["delta"]- 1)/coef(cesNls)["delta"],"\n")

## alpha = 0.7485641

cat("sigma =", 1/(1 - coef(cesNls)["rho"]),"\n")

## sigma = 0.835429

Estimador PPML

#library(gravity)
#PPML("gdp85", c("x1", "x2") ,data = GrowthDJ)

library(RStata)
options("RStata.StataPath" =  
          "\"C:\\Program Files (x86)\\Stata13\\StataMP-64\""
)

options("RStata.StataVersion" = 13)

PPML

ppml <- stata("ppml gdp85 x1 x2", data.in = GrowthDJ, data.out = T)

## . ppml gdp85 x1 x2
## note: checking the existence of the estimates
## note: starting ppml estimation
## 
## Iteration 1:   deviance =  216457.8
## Iteration 2:   deviance =  189591.8
## Iteration 3:   deviance =  187978.6
## Iteration 4:   deviance =  187971.6
## Iteration 5:   deviance =  187971.6
## Iteration 6:   deviance =  187971.6
## 
## Number of parameters: 2
## Number of observations: 98
## Number of observations dropped: 0
## Pseudo log-likelihood: -94470.186
## R-squared: .58293426
## -------------------------------------------------------
## > -----------------------
##              |               Robust
##        gdp85 |      Coef.   Std. Err.      z    P>|z|  
## >    [95% Con                                          
## >            f. Interval]
## -------------+-----------------------------------------
## > -----------------------
##           x2 |  -3.558712   .3502415   -10.16   0.000  
## >   -4.245172                                          
## >               -2.872251
##        _cons |   10.05512   .1438674    69.89   0.000  
## >    9.773144                                          
## >                10.33709
## -------------------------------------------------------
## > -----------------------
## Number of regressors dropped to ensure that the estimat
## > es exist: 1
## Dropped variables:  x1
## Option strict is off

GrowthDJ <- GrowthDJ %>% 
  mutate(lngdp85 = log(gdp85))



nl<- stata("nl (lngdp85 = {b0} - 1/{rho=1}*ln({delta=0.5}*x1^(-1*{rho}) + (1 - {delta})*x2^(-1*{rho})))", 
data.in = GrowthDJ, data.out = F)

## . nl (lngdp85 = {b0} - 1/{rho=1}*ln({delta=0.5}*x1^(-1*
## > {rho}) + (1 - {delta})*x2^(-1*{rho})))
## (obs = 98)
## 
## Iteration 0:  residual SS =  2157.958
## Iteration 1:  residual SS =  1855.725
## Iteration 2:  residual SS =  1312.245
## Iteration 3:  residual SS =  278.2478
## Iteration 4:  residual SS =  44.94087
## Iteration 5:  residual SS =  44.19495
## Iteration 6:  residual SS =  44.19333
## Iteration 7:  residual SS =   44.1933
## Iteration 8:  residual SS =   44.1933
## Iteration 9:  residual SS =   44.1933
## Iteration 10:  residual SS =   44.1933
## Iteration 11:  residual SS =   44.1933
## 
##       Source |       SS       df       MS
## -------------+------------------------------         Nu
## > mber of obs =        98
##        Model |   68.820112     2   34.410056         R-
## > squared     =    0.6090
##     Residual |  44.1932972    95  .465192602         Ad
## > j R-squared =    0.6007
## -------------+------------------------------         Ro
## > ot MSE      =  .6820503
##        Total |  113.013409    97  1.16508669         Re
## > s. dev.     =  200.0653
## 
## -------------------------------------------------------
## > -----------------------
##      lngdp85 |      Coef.   Std. Err.      t    P>|t|  
## >    [95% Con                                          
## >            f. Interval]
## -------------+-----------------------------------------
## > -----------------------
##          /b0 |   6.937532   .1284953    53.99   0.000  
## >    6.682436                                          
## >                7.192627
##         /rho |   .1662469     .10777     1.54   0.126  
## >   -.0477037                                          
## >                .3801975
##       /delta |   2.105344   .2431788     8.66   0.000  
## >    1.622573                                          
## >                2.588115
## -------------------------------------------------------
## > -----------------------
##   Parameter b0 taken as constant term in model & ANOVA 
## > table

alpha <- stata("cat( 'alpha =', (coef(nl)['delta']- 1)/coef(nl)['delta'])")

## . cat( 'alpha =', (coef(nl)['delta']- 1)/coef(nl)['delt
## > a'])
## invalid ''' 
## r(198);

De modo que $α = \frac{δ - 1}{δ} = \frac{1.62 - 1}{1.62} = 0.32$ .

Estimação em Log: Basic Solow CD equation

$\ln (\frac{Y_{i}}{L_{i}}) = \ln A (0) + g t + \frac{α}{1 - α} \ln (\frac{s_{i, k}}{n_{i} + g + δ})$

GrowthDJ <- GrowthDJ %>% 
  mutate(ln_sk = log(GrowthDJ$invest/100)) %>% 
  mutate(ndelta =  (GrowthDJ$popgrowth + 5)/100)


BasicSolowCD <- lm(gdp85 ~ ln_sk + ndelta , data = GrowthDJ)
summary(BasicSolowCD)

## 
## Call:
## lm(formula = gdp85 ~ ln_sk + ndelta, data = GrowthDJ)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -6966.1 -2199.6  -431.2  2486.9 10374.5 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)    32818       2954  11.111  < 2e-16 ***
## ln_sk           5534        726   7.624 1.85e-11 ***
## ndelta       -239899      41600  -5.767 1.00e-07 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 3510 on 95 degrees of freedom
## Multiple R-squared:  0.5668, Adjusted R-squared:  0.5577 
## F-statistic: 62.15 on 2 and 95 DF,  p-value: < 2.2e-16

Temos retornos crescentes e decrescentes de escala, caso $ν > 1$ ou $ν < 1$ , respectivamente.↩︎