Analise de Churn com Tidymodels Parte 1
Introdução
O objetivo do post é apresentar o pacote tidymodels resolvendo um problema simples de customer churn. O tidymodels é uma constelação de pacotes de modelagem estatística e de machine learning presentes no R e que torna simples e prático diversas tarefas presentes no fluxo de trabalho da criação de modelos preditivos. Isto inclui a tarefa de feature engineering dos dados; a criação de conjuntos de teste, treinamento ou folds de cross validation; a estimação e afinamento (tuning) de dezenas de modelos, além do cálculo de diversas medidas de avaliação de performance.
Talvez o principal pacote do tidymodels seja o parsnip. Como sucessor espiritual do caret, seu grande merito é unificar a sintaxe de um gama enorme de modelos estatísticos e de machine learning. Já o pacote rsample tem o objetivo de realizar reamostragens dos dados, como a criação de conjuntos de dados de treinamento e de teste e de folds para realização de cross validation, duas operações importantes para a criação de modelos preditivos.
Mas antes de aplicar qualquer modelo aos dados, podemos utilizar o pacote recipes para criar pequenas receitas de bolo com instruções de pré-processamento dos dados. Ele torna simples tarefas como a criação de variáveis dummies, a normalização de variáveis numéricas, remoção de colunas com variância zero, a criação de variáveis derivadas da coluna de tempo (como dummy de dia, mês, ano e dia da semana), além de muitas outras operações de feature engineering que são tão importantes, mas por vezes tediosas.
Já o yardstick facilita a criação de medidas de performance dos modelos que serão estimados, produzindo as principais medidas de desempenho para problemas de regressão (RMSE, R-Quadrado e outros) e de classificação (matriz de confusão, precisão, acurácia e outros).
Por fim, temos os pacotes tune e dials que facilitam a busca de hiperparâmetros ideais dos modelos e o pacote workflow, que garante que todas as etapas acima possam se comunicar de maneira simples e prática.
O Banco de Dados
Para este projeto vou utilizar uma base de customer churn da Telco. Ela contém 7043 linhas, cada uma representando um cliente, e 20 colunas que representam potenciais preditores da probabilidade de churn. Eles oferecem informações que podem nos ajudar a prever o comportamento dos clientes e a desenvolver programas focados em retenção de clientes.
library(tidyverse)
library(tidymodels)
library(skimr)
library(knitr)
library(doFuture)
data(wa_churn, package = "modeldata")O banco de dados inclui 20 variáveis, sendo 4 numéricas e 16 categóricas. Churn é a nossa variável de interesse, e indica se o cliente abandonou ou não a empresa. Como a ideia é apresentar os procedimentos do tidymodels, não irei passar muito tempo analisando o banco de dados, mas é possível observar que existem 11 observações sem valor definido (missing ou NA) na coluna totalcharges. Nas etapas de pré-processamento podemos tratar estes problemas.
wa_churn %>% skim()| Name | Piped data |
| Number of rows | 7043 |
| Number of columns | 20 |
| _______________________ | |
| Column type frequency: | |
| factor | 11 |
| numeric | 9 |
| ________________________ | |
| Group variables | None |
Variable type: factor
| skim_variable | n_missing | complete_rate | ordered | n_unique | top_counts |
|---|---|---|---|---|---|
| churn | 0 | 1 | FALSE | 2 | No: 5174, Yes: 1869 |
| multiple_lines | 0 | 1 | FALSE | 3 | No: 3390, Yes: 2971, No : 682 |
| internet_service | 0 | 1 | FALSE | 3 | Fib: 3096, DSL: 2421, No: 1526 |
| online_security | 0 | 1 | FALSE | 3 | No: 3498, Yes: 2019, No : 1526 |
| online_backup | 0 | 1 | FALSE | 3 | No: 3088, Yes: 2429, No : 1526 |
| device_protection | 0 | 1 | FALSE | 3 | No: 3095, Yes: 2422, No : 1526 |
| tech_support | 0 | 1 | FALSE | 3 | No: 3473, Yes: 2044, No : 1526 |
| streaming_tv | 0 | 1 | FALSE | 3 | No: 2810, Yes: 2707, No : 1526 |
| streaming_movies | 0 | 1 | FALSE | 3 | No: 2785, Yes: 2732, No : 1526 |
| contract | 0 | 1 | FALSE | 3 | Mon: 3875, Two: 1695, One: 1473 |
| payment_method | 0 | 1 | FALSE | 4 | Ele: 2365, Mai: 1612, Ban: 1544, Cre: 1522 |
Variable type: numeric
| skim_variable | n_missing | complete_rate | mean | sd | p0 | p25 | p50 | p75 | p100 | hist |
|---|---|---|---|---|---|---|---|---|---|---|
| female | 0 | 1 | 0.50 | 0.50 | 0.00 | 0.00 | 0.00 | 1.00 | 1.00 | ▇▁▁▁▇ |
| senior_citizen | 0 | 1 | 0.16 | 0.37 | 0.00 | 0.00 | 0.00 | 0.00 | 1.00 | ▇▁▁▁▂ |
| partner | 0 | 1 | 0.48 | 0.50 | 0.00 | 0.00 | 0.00 | 1.00 | 1.00 | ▇▁▁▁▇ |
| dependents | 0 | 1 | 0.30 | 0.46 | 0.00 | 0.00 | 0.00 | 1.00 | 1.00 | ▇▁▁▁▃ |
| tenure | 0 | 1 | 32.37 | 24.56 | 0.00 | 9.00 | 29.00 | 55.00 | 72.00 | ▇▃▃▃▆ |
| phone_service | 0 | 1 | 0.90 | 0.30 | 0.00 | 1.00 | 1.00 | 1.00 | 1.00 | ▁▁▁▁▇ |
| paperless_billing | 0 | 1 | 0.59 | 0.49 | 0.00 | 0.00 | 1.00 | 1.00 | 1.00 | ▆▁▁▁▇ |
| monthly_charges | 0 | 1 | 64.76 | 30.09 | 18.25 | 35.50 | 70.35 | 89.85 | 118.75 | ▇▅▆▇▅ |
| total_charges | 11 | 1 | 2283.30 | 2266.77 | 18.80 | 401.45 | 1397.47 | 3794.74 | 8684.80 | ▇▂▂▂▁ |
Definindo o Conjunto de Treinamento e Teste: rsample
Antes de partir para o pré-processamento e para a estimação dos modelos, podemos utilizar o pacote rsample para construir um conjunto de treinamento e de teste. O pacote fornece uma série de funções que tornam simples o processo de gerar reamostragens aleatórias para além do split training-test, como boostraps via rsample::bootstraps, a criação de split para séries temporais com a função rsample::initial_time_split e a criação de folds para cross-validation com a função rsample::vfold_cv().
Na segunda parte do post utilizaremos cross-validation para afinar os modelos, mas por enquanto vamos utilizar a função initial_split() para gerar uma base de treinamento com 80% das informações do banco de dados original.
set.seed(123)
tbl_treinamento_teste <- initial_split(data = wa_churn, prop = 0.8)
tbl_treinamento <- tbl_treinamento_teste %>% training()
tbl_teste <- tbl_treinamento_teste %>% testing()
tbl_treinamento_teste## <Analysis/Assess/Total>
## <5635/1408/7043>Do total de 7043 clientes, 5635 foram atribuídos ao conjunto de treinamento e 1408 para o conjunto de teste.
Pré-processando dados: recipes
Como discutido na introdução, o pacote recipes utiliza uma série de funções para lidar com o pré-processamento dos dados. O primeiro passo é informar a formula utilizada na receita, no nosso caso Churn como nossa variável dependente e as demais como preditores. Além de servir como a fórmula dos modelos que vamos estimar, a fórmula também tem o objetivo de permitir o acesso a uma série de funções seletoras bastante convenientes como all_predictors(), que permite aplicar transformações sobre todos os preditores, ou all_outcomes(), que permite transformações sobre os outcomes.
Com step_impute_linear imputamos valores àquelas linhas com observações faltantes na coluna totalCharge. Com step_dummy queremos criar uma série de colunas dummies a partir dos preditores categoricos. Para não informar cada coluna manualmente, podemos utilizar a função selectora all_nominal, além de informar à função step_dummy que ignore os outcomes. Logo, nossas 16 variáveis categóricas dão lugar a outras tantas colunas dummies. Por fim, vamos normalizar os valores das variáveis numéricas utilizando step_normalize.
receita_simples <- recipe(churn ~ ., data = tbl_treinamento) %>%
step_impute_linear(all_numeric()) %>%
step_dummy(all_nominal(), -all_outcomes()) %>%
step_normalize(all_numeric())Note que muitas outras funções de transformação estão incluidas no pacote recipe, permitindo a ímputação de valores missings pela média step_meanimpute; as transformações log (step_log) e quadrática (step_sqrt) das variáveis, a especificação genérica da função dplyr::mutate com step_mutate, a discretização de variáveis numéricas com step_cut, a geração de variáveis de data com step_date (dummies de dia, mês, ano, e dia da semana) e muitas outras. Uma lista de todas as transformações possíveis pode ser obtida na documentação do recipe.
Para exibir como o banco de dados ficou após as transformações, Chamamos prep(), que aplica a receita ao banco de dados, e utilizamos juice() para extrair o banco de dados transformado.
receita_simples %>% prep() %>% juice() %>% skim()| Name | Piped data |
| Number of rows | 5635 |
| Number of columns | 31 |
| _______________________ | |
| Column type frequency: | |
| factor | 1 |
| numeric | 30 |
| ________________________ | |
| Group variables | None |
Variable type: factor
| skim_variable | n_missing | complete_rate | ordered | n_unique | top_counts |
|---|---|---|---|---|---|
| churn | 0 | 1 | FALSE | 2 | No: 4155, Yes: 1480 |
Variable type: numeric
| skim_variable | n_missing | complete_rate | mean | sd | p0 | p25 | p50 | p75 | p100 | hist |
|---|---|---|---|---|---|---|---|---|---|---|
| female | 0 | 1 | 0 | 1 | -0.98 | -0.98 | -0.98 | 1.02 | 1.02 | ▇▁▁▁▇ |
| senior_citizen | 0 | 1 | 0 | 1 | -0.45 | -0.45 | -0.45 | -0.45 | 2.23 | ▇▁▁▁▂ |
| partner | 0 | 1 | 0 | 1 | -0.97 | -0.97 | -0.97 | 1.03 | 1.03 | ▇▁▁▁▇ |
| dependents | 0 | 1 | 0 | 1 | -0.66 | -0.66 | -0.66 | 1.52 | 1.52 | ▇▁▁▁▃ |
| tenure | 0 | 1 | 0 | 1 | -1.32 | -0.95 | -0.14 | 0.96 | 1.60 | ▇▃▃▃▆ |
| phone_service | 0 | 1 | 0 | 1 | -3.09 | 0.32 | 0.32 | 0.32 | 0.32 | ▁▁▁▁▇ |
| paperless_billing | 0 | 1 | 0 | 1 | -1.20 | -1.20 | 0.83 | 0.83 | 0.83 | ▆▁▁▁▇ |
| monthly_charges | 0 | 1 | 0 | 1 | -1.53 | -0.98 | 0.19 | 0.84 | 1.79 | ▇▅▆▇▅ |
| total_charges | 0 | 1 | 0 | 1 | -1.57 | -0.83 | -0.39 | 0.66 | 2.80 | ▇▇▃▃▂ |
| multiple_lines_No.phone.service | 0 | 1 | 0 | 1 | -0.32 | -0.32 | -0.32 | -0.32 | 3.09 | ▇▁▁▁▁ |
| multiple_lines_Yes | 0 | 1 | 0 | 1 | -0.86 | -0.86 | -0.86 | 1.17 | 1.17 | ▇▁▁▁▆ |
| internet_service_Fiber.optic | 0 | 1 | 0 | 1 | -0.88 | -0.88 | -0.88 | 1.13 | 1.13 | ▇▁▁▁▆ |
| internet_service_No | 0 | 1 | 0 | 1 | -0.53 | -0.53 | -0.53 | -0.53 | 1.88 | ▇▁▁▁▂ |
| online_security_No.internet.service | 0 | 1 | 0 | 1 | -0.53 | -0.53 | -0.53 | -0.53 | 1.88 | ▇▁▁▁▂ |
| online_security_Yes | 0 | 1 | 0 | 1 | -0.64 | -0.64 | -0.64 | 1.57 | 1.57 | ▇▁▁▁▃ |
| online_backup_No.internet.service | 0 | 1 | 0 | 1 | -0.53 | -0.53 | -0.53 | -0.53 | 1.88 | ▇▁▁▁▂ |
| online_backup_Yes | 0 | 1 | 0 | 1 | -0.72 | -0.72 | -0.72 | 1.39 | 1.39 | ▇▁▁▁▅ |
| device_protection_No.internet.service | 0 | 1 | 0 | 1 | -0.53 | -0.53 | -0.53 | -0.53 | 1.88 | ▇▁▁▁▂ |
| device_protection_Yes | 0 | 1 | 0 | 1 | -0.72 | -0.72 | -0.72 | 1.38 | 1.38 | ▇▁▁▁▅ |
| tech_support_No.internet.service | 0 | 1 | 0 | 1 | -0.53 | -0.53 | -0.53 | -0.53 | 1.88 | ▇▁▁▁▂ |
| tech_support_Yes | 0 | 1 | 0 | 1 | -0.63 | -0.63 | -0.63 | 1.58 | 1.58 | ▇▁▁▁▃ |
| streaming_tv_No.internet.service | 0 | 1 | 0 | 1 | -0.53 | -0.53 | -0.53 | -0.53 | 1.88 | ▇▁▁▁▂ |
| streaming_tv_Yes | 0 | 1 | 0 | 1 | -0.79 | -0.79 | -0.79 | 1.27 | 1.27 | ▇▁▁▁▅ |
| streaming_movies_No.internet.service | 0 | 1 | 0 | 1 | -0.53 | -0.53 | -0.53 | -0.53 | 1.88 | ▇▁▁▁▂ |
| streaming_movies_Yes | 0 | 1 | 0 | 1 | -0.80 | -0.80 | -0.80 | 1.25 | 1.25 | ▇▁▁▁▅ |
| contract_One.year | 0 | 1 | 0 | 1 | -0.52 | -0.52 | -0.52 | -0.52 | 1.93 | ▇▁▁▁▂ |
| contract_Two.year | 0 | 1 | 0 | 1 | -0.57 | -0.57 | -0.57 | -0.57 | 1.77 | ▇▁▁▁▂ |
| payment_method_Credit.card..automatic. | 0 | 1 | 0 | 1 | -0.52 | -0.52 | -0.52 | -0.52 | 1.93 | ▇▁▁▁▂ |
| payment_method_Electronic.check | 0 | 1 | 0 | 1 | -0.70 | -0.70 | -0.70 | 1.43 | 1.43 | ▇▁▁▁▃ |
| payment_method_Mailed.check | 0 | 1 | 0 | 1 | -0.55 | -0.55 | -0.55 | -0.55 | 1.81 | ▇▁▁▁▂ |
Agora temos uma variável categórica, que é a resposta do modelo, e 30 variáveis numéricas, a maioria delas criadas a partir da transformação step_dummy.
Ajustando modelos: parsnip
Finalmente, após as etapas de pré-processamento dos dados e a criação de um conjunto de treinamento e teste podemos utilizar o pacote parsnip para estimar alguns modelos.
Como discutimos na introdução, o parsnip realiza um trabalho incrível de unificar uma série de diferentes modelos estatísticos e de machine learning em um único ambiente. O pacote é extremamente conveniente porque permite que o usuário utilize uma única forma de se comunicar com diferentes modelos que inicialmente possuiam sintaxes totalmente diferentes ou exigiam dados em diferentes formatos (matrix, ts, data.frame).
Para utilizar o parsnip, sempre começamos definindo o modelo. Assim, para estimar uma regressão linear utilizamos a função linear_reg() e para estimar um random forest utilizamos a função rand_forest(). Contudo, muitos outros modelos estão presentes, como o modelo ARIMA (arima_reg), o modelo prophet (prophet_reg), Support Vector Machines (svm_poly e svm_rbf), regressão logística (logistic_reg), KNN (nearest_neighbor) e muitos outros. Uma lista completa de todos os modelos suportados pode ser encontrada na documentação do parsnip.
Definido o modelo, devemos informar a implementação do algorítimo, que é definida pela função set_engine(). Assim, ao rodar um modelo de Random Forest podemos utilizar a implementação do pacote randomForest, com set_engine("randomForest"), a implementação do pacote ranger com set_engine("ranger") ou do spark com set_engine("spark"). Mais uma vez reforço a conveniência do parsnip. Em cada um dos pacotes, os hiperparâmetros são nomeados de maneiras diferentes, como n.trees no ranger e trees no randomForest, mas o parsnip unifica essas sintaxes e utiliza o mesmo nome para os hiperparâmetros.
Para nossos dados, podemos estimar um modelo de Random Forest. Nenhuma razão específica nesta escolha, a não ser que ele é um modelo bastante popular para o problema de classificação que temos. O pacote workflowset é uma alternativa interessante para quando precisamos estimar vários modelos diferentes, com diferentes especificações (ou recipes). Mas por simplicidade, vamos continuar com um único modelo.
modelo_rf <-
rand_forest(mtry = 3, trees = 200, min_n = 30) %>%
set_mode("classification") %>%
set_engine("ranger")
modelo_rf## Random Forest Model Specification (classification)
##
## Main Arguments:
## mtry = 3
## trees = 200
## min_n = 30
##
## Computational engine: rangerAssim, para ajustar o modelo de random forest aos dados, definimos o modelo com a função rand_forest() especificando três hiperparâmetros do modelo: mtry, trees e min_n. Como o modelo de árvore aleatória é uma ensemble (conjunto) de modelos de árvore de decisão, precisamos definir o número de árvores com trees. Além disto, quando criamos uma árvore, um número fixo de variáveis (mtry) é escolhido aleatoriamente quando um nó se divide em dois (split). Enquanto que min_n representa o número mínimo de observações que devem existir em um nó para que o modelo de árvore de decisão continue produzindo splits.
Neste primeiro momento, vamos fixar estes valores com base no nosso achismo, e declara-los na função rand_forest. Depois informamos em set_mode que desejamos estimar um modelo de classificação (e não de regressão), por fim, escolhemos a implementação do algorítimo de random forest com set_engine.
Combinando tudo: workflows
Agora temos os três ingredientes mais importantes para nosso modelo preditivo: (1) temos as bases de treinamento e teste, (2) temos uma receita de bolo com o passo-a-passo do pré-processamento que deve ser aplicado em todas as bases de dados; e (3) declaramos o modelo que deve ser ajustado. Para facilitar a integração de todas essas peças, podemos utilizar o pacote workflows.
Iniciamos um workflow sempre com a função workflow(). Adicionamos o modelo definido acima com add_model e a receita que deve ser aplicada aos dados com add_recipe. O último passo é o fit, onde passamos a base de treinamento construida pelo pacote rsample para que o random forest seja estimado.
workflow_rf <- workflow() %>%
add_model(modelo_rf) %>%
add_recipe(receita_simples) %>%
fit(training(tbl_treinamento_teste))
workflow_rf## == Workflow [trained] ==========================================================
## Preprocessor: Recipe
## Model: rand_forest()
##
## -- Preprocessor ----------------------------------------------------------------
## 3 Recipe Steps
##
## * step_impute_linear()
## * step_dummy()
## * step_normalize()
##
## -- Model -----------------------------------------------------------------------
## Ranger result
##
## Call:
## ranger::ranger(x = maybe_data_frame(x), y = y, mtry = min_cols(~3, x), num.trees = ~200, min.node.size = min_rows(~30, x), num.threads = 1, verbose = FALSE, seed = sample.int(10^5, 1), probability = TRUE)
##
## Type: Probability estimation
## Number of trees: 200
## Sample size: 5635
## Number of independent variables: 30
## Mtry: 3
## Target node size: 30
## Variable importance mode: none
## Splitrule: gini
## OOB prediction error (Brier s.): 0.1347099Assim, é possível observar que o modelo foi ajustado para as 5635 observações do conjunto de treinamento. O número de variáveis independentes é igual a 30, como resultado da aplicação da receita sobre as variáveis do banco de dados original. Em Call observamos que nossos dados foram aplicados na função ranger::ranger(), como definido no set_engine().
Avaliando a Performance do Modelo: yardstick
O último passo é calibrar o modelo no conjunto de teste e construir medidas de performance do modelo a partir da comparação dos valores previstos e dos valores verdadeiros. Para tanto utilizamos o pacote yardstick e sua função conf_mat() para a construção da matriz de confusão. Para problemas de regressão é possível utilizar a função metrics(), que retorna medidas como RMSE, MAE e R-Quadrado.
A partir do modelo ajustado que está armazenado no objeto workflow_rf, utilizamos a função predict para produzir o vetor de valores previstos. Com bind_cols criamos um data.frame com valores previstos e os dados observados da base de teste.
É importante destacar que a base teste sofrerá as mesmas transformações que foram aplicadas na base de treinamento. Isso ocorre porque new_data em predict está herdando a receita de workflow_rf.
Munido dos dados previstos e dos dados observados, a função conf_mat pode construir nossa matriz de confusão:
matriz_confusao <- workflow_rf %>%
predict(new_data = testing(tbl_treinamento_teste)) %>%
bind_cols(testing(tbl_treinamento_teste) %>% select(churn)) %>%
mutate_all(as.factor) %>%
conf_mat(churn, .pred_class)
matriz_confusao %>%
pluck(1) %>%
as_tibble() %>%
ggplot(aes(Prediction, Truth, alpha = n)) +
geom_tile(show.legend = FALSE) +
labs(x = "Previsto", y = "Observado") +
geom_text(aes(label = n), color = 'white', alpha = 1, size = 8)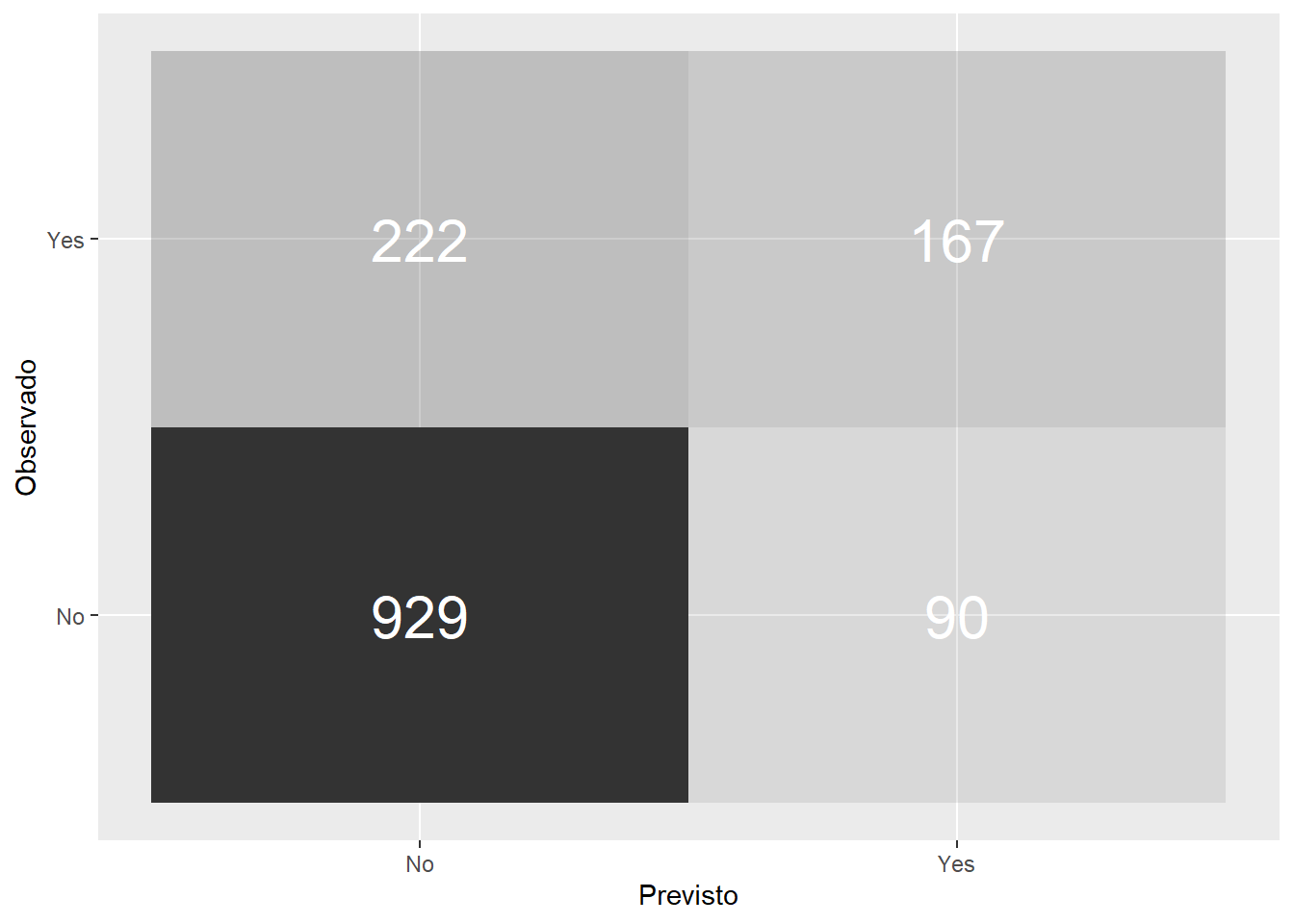
A matriz de confusão mostra que o modelo erroneamente previu como negativo 222 clientes que iriam abandonar a empresa. E previu incorretamente que 90 clientes iriam sair da empresa quando na verdade eles permaneceram como clientes.
A partir da matriz de confusão podemos estimar algumas medidas de performance, como acurácia, precisão e recall.
matriz_confusao %>%
summary() %>%
select(-.estimator) %>%
filter(.metric %in% c('precision', 'recall', 'f_meas',
'accuracy', 'spec', 'sens')) %>%
rename(Medida = 1, Estimativa = 2) %>%
kable()| Medida | Estimativa |
|---|---|
| accuracy | 0.7784091 |
| sens | 0.4293059 |
| spec | 0.9116781 |
| precision | 0.6498054 |
| recall | 0.4293059 |
| f_meas | 0.5170279 |
A acurácia do modelo é a fração de previsões que o modelo fez corretamente. Contudo, acurácia não é uma medida muito confiável como ela pode produzir resultados incorretos se a base de dados for muito desbalanceada. No caso, nosso modelo random Forest produziu uma acurácia de 78%. Contudo, 73% das observações no banco de dados são negativas.
Já a precisão mostra o quanto o modelo é sensível a falsos positivos (FP), como prever que um cliente está abandonando a empresa quando na verdade ele vai permanecer. O recall procura mostrar o quão sensível o modelo é a falsos negativos (FN), como prever que o cliente irá permanecer quando na verdade ele está saindo.
Estas duas medidas são mais relevantes no contexto de uma empresa, dado que a firma está interessada em prever de maneira precisa quais clientes realmente estão em risco de se desligar. A previsão correta garante que a empresa pode conduzir estratégias de retenção com estes clientes, ao mesmo tempo que minimiza a possibilidade de aplicar esforços de retenção sob clientes falsos positivos.
Outra medida popular é o F1 Score, que é uma média harmônica da precisão e do recall. Um F1 score obtém seu melhor valor em 1 quando se tem um recall e precisão perfeitos. O nosso modelo obteve um F1 de 0,85. Por fim, temos a medida de UAC-ROC, que vamos utilizar na próxima seção para escolher o melhor modelo.
Conclusão
O tidymodels e seus pacotes tornam muito simples a tarefa de aplicar modelos estatísticos e de machine learning para bases de dados. Desde o pré-processamento com recipes, a produção de reamostragens com o rsample, a estimação de modelos com parsnip, a avaliação da qualidade das previsões com yardstick e a criação de workflows com workflow.
Na próxima parte desta série, vamos analisar o afinamento do modelo de random forest utilizando os pacotes tune e dials.